최신보고서

목차
Ⅰ. 서론
Ⅱ. 이론적 배경
Ⅲ. 실증 분석
1. 방법론
2. 데이터
3. 실증 분석 결과
Ⅳ. 시나리오 분석
1. 방법론
2. 시나리오 분석 결과
Ⅴ. 요약 및 결론
Ⅱ. 이론적 배경
Ⅲ. 실증 분석
1. 방법론
2. 데이터
3. 실증 분석 결과
Ⅳ. 시나리오 분석
1. 방법론
2. 시나리오 분석 결과
Ⅴ. 요약 및 결론
- 요약
- 이론적으로 주식 수익률은 실물 경제활동을 반영하는 자본투자 수익률과 밀접하게 연관되어 있다. 본 연구는 자본투자 수익률이 주식 수익률의 중장기적인 흐름을 잘 설명할 수 있음을 실증적으로 보이고, 자본투자 수익률을 결정했던 그간의 경제환경에 대해 조망한다. 아울러 인구와 노동시장 변화 등에 대한 시나리오를 바탕으로 향후 자본투자 수익률에 대한 전망 결과를 함께 제시하고자 한다. 이러한 분석을 통해 장기적인 시각에서 주식 시장의 추세적 동인에 대한 이해를 돕는 것이 본 연구의 목적이다.
1980년대 이후 국내외 경제환경에는 많은 변화가 있었다. 국내적으로는 1990년대 중반까지 인적·물적 자본이 빠르게 축적되었는데, 그 과정에서 기업 부문의 부실과 비효율이 누적되었고, 외환위기를 계기로 대규모 구조조정이 단행되었다. 대외적으로는 1990년대 들어 각국의 세계화와 경제 개방이 본격적으로 진행되면서 글로벌 분업과 경쟁이 본격화되었다. 한편, 이러한 흐름 이후를 내다볼 때, 다가올 국내 경제환경 변화 중 가장 중요한 것으로 인구 감소와 고령화를 들 수 있다. 2021년에 발표된 통계청의 인구 전망(중위)에 따르면, 핵심 경제활동 연령대인 25~49세의 인구는 2024년 이후 20년간 약 24% 감소할 것으로 예상된다. 그리고 동 기간 중 65세 이상 인구의 비중은 2배 가까이 증가할 것으로 전망된다.
실증 분석에 따르면, 2000년 이후 자본투자 수익률은 이전에 비해 평균적으로 하락한 것으로 나타났다. 이는 고도 성장기가 저물고 저성장 국면으로 진입한 데 따른 자명한 결과로 인식될 수도 있다. 하지만, 자본투자 수익률의 구성 요소에 대해 세부적으로 살펴보면 보다 흥미로운 결과를 발견할 수 있다. 자본투자 수익률은 크게 최종재 산출을 통해 얻는 생산 측면의 수익률과 자본의 가치에 대한 평가를 통해 얻는 보유가치 측면의 수익률로 구분할 수 있다. 두 구성 요소를 기간별로 보면, 2000년대 들어 생산 측면의 수익률이 소폭 상승했다는 점이 특징적이다. 여기에는 자본투입의 효율이 감소하기는 했지만, 자본을 보다 저렴한 비용으로 구입할 수 있게 된 점이 배경으로 작용하였다. 그리고 자본재의 가격이 낮아진 것은 세계화에 따른 접근성 개선과 산업 정책(제조업 육성)으로 인한 공급 확대 등에 기인한 결과로 생각된다. 반면, 보유가치 측면의 수익률은 2000년대 들어 전반적으로 하락하였는데, 여기에는 투자 이후 유효하게 잔존하는 자본(자본 잔존도)의 감소가 큰 영향을 미쳤다. 1990년 이후 자본 잔존도를 보면, 외환위기 당시 크게 낮아진 후 전반적으로 하락한 모습이 나타난다. 이처럼 자본의 잔존도가 감소한 것은 대규모 구조조정, 노동 공급의 정체, 성장잠재력 축소 등으로 인해 적극적인 투자를 통해 이를 유지하는 데에 한계가 있었기 때문으로 판단된다.
위의 실증 분석과 함께, 인구 시나리오를 바탕으로 향후 20년간의 자본투자 수익률을 전망한 결과는 다음과 같다. 먼저, 통계청의 중위 인구 전망을 이용한 시나리오 분석 결과에 따르면, 인구 증가율과 자본투자 수익률은 시계열적으로 상당히 유사한 방향성을 가진다는 특징이 있었다. 아울러 인구 수준별 시나리오에 따르면, 20년 후 고위와 저위 인구의 누적수익률은 중위 인구 대비 약 ±20%p에 가까운 격차를 나타내는 것으로 분석되었다. 이상의 결과들은, 인구 변화가 구조적인 요인으로 작용하면서 그 전개 방향이 자본투자 수익률에 큰 영향을 미칠 것이라는 점을 의미한다.
전술한 시나리오 분석은 인구를 제외한 연령별·성별 경제활동 참가 정도는 현재와 동일하다는 가정을 바탕으로 한다. 하지만, 현실적으로는 인적 자본의 고도화, 정책 및 경제활동 여건의 개선 등으로 노동시장 참여도가 변화할 가능성을 배제할 수 없다. 이러한 점을 고려하여 50~64세 인구와 여성의 노동 공급이 매년 0.5%p씩 20년간 총 7%p와 10%p 증가하는 경우를 각각 가정하여 분석하였다. 이 경우 자본투자 수익률(누적)은 기본 시나리오 대비 24%p와 36%p 높아지는 것으로 나타났다.
실물 경제뿐만 아니라 주식 시장의 지속적인 성장을 위해서도 기술 진보와 생산성 향상의 중요성은 분명히 강조되어야 한다. 하지만 노동시장 참여 여건을 개선함으로써 기술 진보를 보완할 수 있는 가능성에 대해서도 주목할 필요가 있다. 특히, 앞서 고연령층 및 여성의 노동 공급 증가를 가정한 시나리오에서의 수익률은 총요소생산성 증가율이 20년간 총 0.3%p 상승하는 경우보다 더 높은 것으로 나타났다. 2000년 이후의 총요소생산성 증가율이 1980~1990년대의 절반 수준으로 낮아졌다는 점을 고려할 때, 총요소생산성 증가율 추세의 상승 전환은 쉽지 않은 과제이다. 이러한 의미에서 위의 결과는 노동시장에 대한 개선을 병행함으로써 기술 발전 둔화를 보완해 나가야 한다는 시사점을 제공한다.
고연령층과 여성의 노동시장 참여는 가용 노동자원을 확대할 수 있는 주요 원천이지만, 이를 단기간에 크게 끌어올리는 것은 쉽지 않다. 하지만, 본 연구의 분석은 점진적인 개선도 중요한 동력으로 작용하면서 자본투자 수익률을 크게 제고할 수 있다는 점을 시사한다. 아울러 고연령층과 여성의 경제활동이 활성화된 주요국의 사례에 비추어 볼 때, 효율적인 정책 개발과 실행이 뒷받침된다면 긍정적인 시나리오가 현실화될 수 있을 것이다.
Ⅰ. 서론
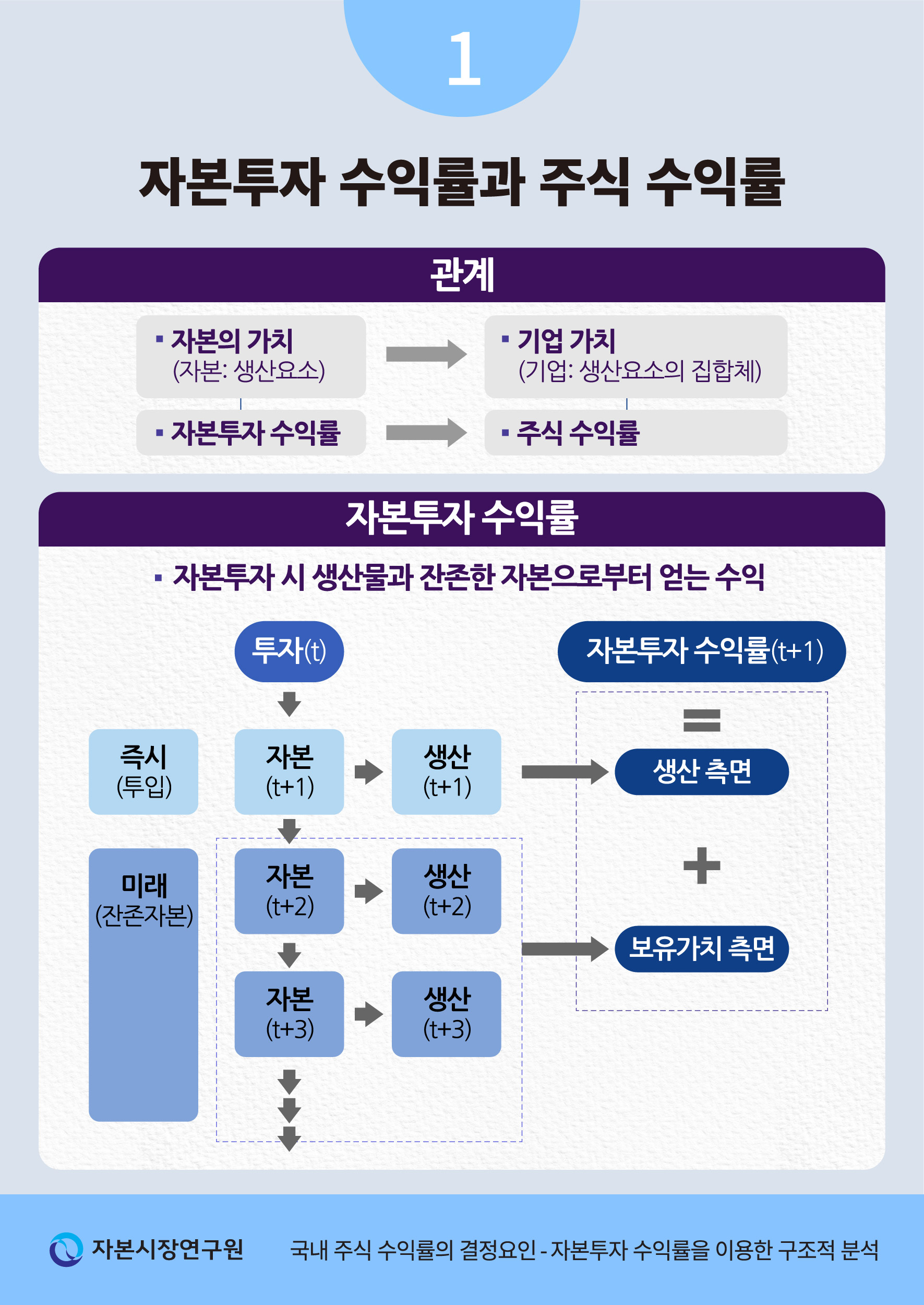
거시적인 관점에서 주식 수익률은 실물 부문, 특히 기업의 자본투자 수익률(capital investment return)과 밀접하게 연관되어 있다. 기업의 자본은 투자를 통해 축적된 생산요소로서 수익을 지속적으로 창출하는 자산이다. 기업을 생산요소의 집합체로 단순화하여 생각한다면, 기업의 가치는 자본의 가치에 직결되면서 주식 수익률은 자본투자 수익률에 따라 움직이는 것으로 볼 수 있다. 본 연구는 이러한 관점에서 1980년 이후 우리나라의 주식 수익률을 자본투자 수익률을 통해 분석하고 20년 시계의 장기 전망을 제시한다.
1980년대 이후 국내외 경제환경에는 많은 변화가 있었다. 국내적으로 1990년대 중반까지의 고도 성장기에는 기업들의 사업 범위가 크게 확장되면서 인적·물적 자본도 빠르게 축적되었다. 하지만 그 과정에서 기업 부문의 부실과 비효율이 누적되었고, 외환위기를 계기로 대규모 구조조정이 뒤따랐다. 대외적으로는 1990년대 들어 각국의 세계화와 경제 개방이 본격적으로 진행되면서 글로벌 분업과 경쟁이 본격화되었다. 그 결과 거래비용이 감소하고 원자재나 자본재 등 생산요소에 대한 접근성도 한층 높아졌다. 이러한 변화가 미친 영향은 실물 경제활동과 직접적으로 연결된 자본투자 수익률에도 반영되어 있을 것으로 생각된다.
한편, 앞으로의 흐름을 내다볼 때, 다가올 국내 경제환경 변화 중 가장 중요한 것으로 인구 감소와 고령화를 들 수 있다. 2021년에 발표된 통계청의 인구 전망(중위)에 따르면, 경제활동이 가장 활발한 연령대인 25~49세의 인구는 2024년 이후 20년간 약 24% 감소할 것으로 예상된다. 또한 65세 이상 인구의 비중은 2024년 19.4%에서 2043년 36.1%로 2배 가까이 증가할 것으로 전망된다. 장비 및 자동화 등을 통한 대체가 어려울 경우, 핵심 경제활동 인구의 감소는 생산 설비 운영이나 서비스 공급 인력의 부족으로 이어지고 자본투자 수익률에도 영향을 미칠 수 있다. 따라서 본 연구는 인구 전망을 바탕으로 향후 국내 자본투자 수익률에 대해 전망하고 시나리오별로 비교·분석하고자 한다. 여기에서는 중위 인구 전망을 기본 시나리오로 하되, 인구 전반, 고연령 계층 및 여성의 노동시장 참여, 총요소생산성 증가율에 대한 시나리오도 함께 고려하여 그 결과를 분석하였다.
이론적인 측면에서 본 연구는 Cochrane(1991)과 Restroy & Rockinger(1994)의 연구를 배경으로 한다. Cochrane(1991)은 자본투자 수익률을 이론적으로 도출하고, 자본투자 수익률이 주식 수익률과 높은 양(+)의 상관관계를 보인다는 실증 분석 결과를 제시한 바 있다. 그리고 Restroy & Rockinger(1994)는 일정한 가정 하에서 주식 수익률과 자본투자 수익률이 이론적으로 동일하다는 점을 보였다. 본 연구의 분석은 이들 연구에서 밝혀진 주식 수익률과 자본투자 수익률 간의 연관성에 기초하고 있다. 아울러 본 연구는 모형 등 기본적인 접근 방법에서 Jermann(1998), Kaltenbrunner & Lochstoer(2010), Croce(2014) 등과도 유사한 측면이 있다. 하지만, 상기 연구들은 추정보다는 이론적 기제와 수치적 실험을 통해 주식 프리미엄 퍼즐을 해결하는 데 초점을 맞추고 있어 목적상 차이가 있다. 한편, 미국을 대상으로 한 Farhi & Gourio(2018)는 연구 목적에 있어 본 연구와 어느 정도 공통점을 가진다. 해당 연구는 1980년대 중반 이후 자본수익률과 무위험이자율의 장기적 추이에 관심을 가지고 생산요소와 시장지배력 등의 구조적 측면을 통해 분석하였다. 다만 본 연구와는 달리, Farhi & Gourio(2018)에서는 주식 수익률과의 연관성에 대한 평가 없이 자본투자 수익률만 독립적으로 분석되었고 장기 전망도 포함되지 않았다.
우리나라의 경우, 주식 수익률에 대해 위와 같은 접근 방식으로 장기적인 시각에서 분석한 연구는 부족한 실정이다. 이러한 측면에서 본 연구는 국내 주식 수익률과 자본투자 수익률 간의 관계, 그리고 자본투자 수익률의 동인이 된 경제환경을 조망하기 위한 참고 자료가 될 수 있을 것으로 생각된다. 본 연구가 제시하는 주요 결과 중 하나로, 자본투자 수익률이 중장기 주식 수익률에 대해 실증적으로 높은 설명력을 가진다는 점을 들 수 있다. 이는 특수한 가정 없이 표준적인 거시 모형을 통해 도출되었기 때문에 국내 자산 가격(asset pricing) 연구에 의미 있게 기여할 수 있을 것으로 생각된다. 아울러 자본투자 수익률에 대한 장기 전망은 노동시장과 관련된 정책적 시사점과 함께, 모형의 폭넓은 활용 가능성을 보여준다는 점에서도 의의를 가진다고 생각된다.
본고의 구성은 다음과 같다. 먼저, Ⅱ장에서는 자본투자 수익률에 대한 이론적인 배경을 제시하고 구성 요소들의 경제적 의미에 대해 설명한다. Ⅲ장에서는 실증 분석을 통해 1980년 이후 우리나라의 자본투자 수익률을 추정하고, 주식 수익률과의 관계 등 주요 특징에 대해 논의하도록 하겠다. 그리고 Ⅳ장에서는 경제환경 변화에 대한 여러 시나리오를 바탕으로 향후 국내 자본투자 수익률에 대해 전망하고 결과를 비교한다. 마지막으로 Ⅴ장에서는 분석 결과와 시사점에 대해 종합적으로 논의하면서 보고서를 맺도록 하겠다.
II. 이론적 배경
자본투자 수익률은 보편적인 거시 모형을 바탕으로 하여 도출된다. 모형에는 무한 계획기간(infinite time horizon) 하에서 최종재를 생산하는 대표 기업이 존재한다. 그리고 이 경제에서는 총요소생산성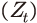 이 외생적으로 주어지고 기업의 투자에 자본조정비용이 수반되는 것으로 가정한다. 이러한 환경 하에서 기업은 매 t기마다 가치(
이 외생적으로 주어지고 기업의 투자에 자본조정비용이 수반되는 것으로 가정한다. 이러한 환경 하에서 기업은 매 t기마다 가치(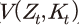 , value function)를 극대화하는 생산요소 투입량을 아래와 같이 결정하게 된다.
, value function)를 극대화하는 생산요소 투입량을 아래와 같이 결정하게 된다.
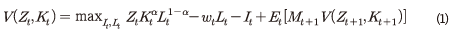
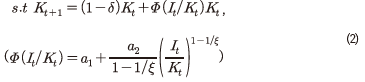
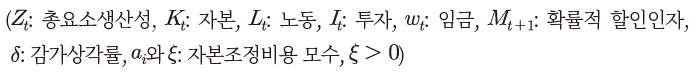
식 (1)은 기업의 목적함수로 우변에 있는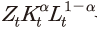 는 기업의 생산함수
는 기업의 생산함수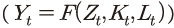 에 해당한다. 이는 통상적인 가정에 따라 규모에 대한 수확불변(constant returns to scale)인 콥-더글라스 생산함수로 설정되었다. 식 (1) 우변의 두 번째
에 해당한다. 이는 통상적인 가정에 따라 규모에 대한 수확불변(constant returns to scale)인 콥-더글라스 생산함수로 설정되었다. 식 (1) 우변의 두 번째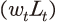 및 세 번째 항
및 세 번째 항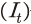 은 노동 비용과 투자인데, 생산에서 이들을 차감한 항
은 노동 비용과 투자인데, 생산에서 이들을 차감한 항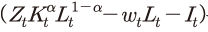 은 배당
은 배당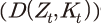 에 해당한다. 그리고 마지막 항인
에 해당한다. 그리고 마지막 항인 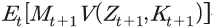 는 일반적으로 계속 가치(continuation value)로 정의된다. 기업은 무한 계획기간 하에서 다음 기에도 동일한 형태의 최적화 문제를 풀게 되므로 이 항이 가산되고 목적함수는 축차적인(recursive) 형태를 띠게 된다. 여기에서 미래의 총요소생산성은 확률적으로 주어지기 때문에 계속 가치는 기댓값으로 결정되게 된다.
는 일반적으로 계속 가치(continuation value)로 정의된다. 기업은 무한 계획기간 하에서 다음 기에도 동일한 형태의 최적화 문제를 풀게 되므로 이 항이 가산되고 목적함수는 축차적인(recursive) 형태를 띠게 된다. 여기에서 미래의 총요소생산성은 확률적으로 주어지기 때문에 계속 가치는 기댓값으로 결정되게 된다.
목적함수 아래에 있는 식 (2)는 제약조건으로 자본축적식을 나타내고 있다. 앞서 언급한 바와 같이 본 모형에서는 실물 부문의 마찰 요인으로 투자에 대한 자본조정비용이 존재하는데, 그 함수적인 형태는 Jermann(1998), Boldrin et al.(2001), Kaltenbrunner & Lochstoer(2010), Croce(2014) 등과 동일하게 설정된다. 자본조정비용의 구체적인 형태는 식 (2)를 변형하여 정리한 식 (3)에서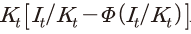 로 표현된 항이다. 자본조정비용이 존재하지 않는 경우의 자본축적식은
로 표현된 항이다. 자본조정비용이 존재하지 않는 경우의 자본축적식은 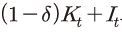 로 감가상각 후 잔존 자본에 신규 투자가 추가되는 형태가 된다.
로 감가상각 후 잔존 자본에 신규 투자가 추가되는 형태가 된다.
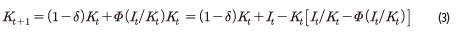
노동의 경우, Jermann(1998), Kaltenbrunner & Lochstoer(2010) 등에서처럼 가계가 여가에 가치를 부여하지 않는다는 단순화 가정을 이용한다. 이에 따라 본 모형에서는 노동의 부존량과 투입량이 일치하게 되므로 기업의 가치 극대화는 최적 투자를 결정하는 문제로 귀결된다.
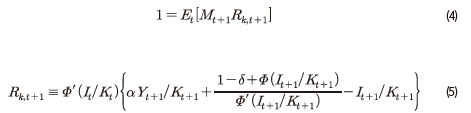
이상의 모형 설정을 바탕으로 기업의 문제를 풀면, 최적화 조건은 식 (4)와 같은 오일러 방정식(Euler equation)으로 압축될 수 있다.1) 식 (4)에서 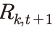 는 자본투자 수익률로, 구체적인 형태는 식 (5)와 같이 정의된다. 여기에서 제약조건인 식 (2)에 대한 라그랑지 승수를
는 자본투자 수익률로, 구체적인 형태는 식 (5)와 같이 정의된다. 여기에서 제약조건인 식 (2)에 대한 라그랑지 승수를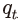 로 두면 일계 조건(first order condition)에 의해
로 두면 일계 조건(first order condition)에 의해 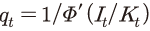 가 도출되는데 이는 최종재에 대한 자본재의 상대가격이 된다.2) 그리고 식 (5)를
가 도출되는데 이는 최종재에 대한 자본재의 상대가격이 된다.2) 그리고 식 (5)를 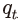 와를
와를 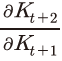 이용하여 정리하면, 자본투자 수익률은 식 (6)과 같이 표현될 수 있다.
이용하여 정리하면, 자본투자 수익률은 식 (6)과 같이 표현될 수 있다.
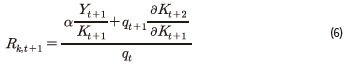
식 (6)의 분자에 위치한 첫 번째 항 은 자본의 한계생산성, 즉, 자본투입 증가를 통해 추가로 산출되는 한계생산물(marginal product)에 해당한다. 따라서 자본의 한계생산성을 t기 자본재의 가격(분모,
은 자본의 한계생산성, 즉, 자본투입 증가를 통해 추가로 산출되는 한계생산물(marginal product)에 해당한다. 따라서 자본의 한계생산성을 t기 자본재의 가격(분모, 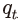 )으로 나누면 그 값은 다음 기(t+1)의 생산을 통해 얻는 수익률로 해석할 수 있다. 그리고 분자에 위치한 두 번째 항에서
)으로 나누면 그 값은 다음 기(t+1)의 생산을 통해 얻는 수익률로 해석할 수 있다. 그리고 분자에 위치한 두 번째 항에서 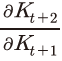 는 t+1기에 자본이 축적됨에 따라 t+2기에 추가적으로 자본이 증가하는 부분을 나타낸다. 이는 t+1기에 축적된 자본이 그 다음기에 잔존하는 양을 의미하는 것으로도 해석할 수 있다. 이러한 잔존 자본에 t+1기의 자본재 가격을 곱한 값
는 t+1기에 자본이 축적됨에 따라 t+2기에 추가적으로 자본이 증가하는 부분을 나타낸다. 이는 t+1기에 축적된 자본이 그 다음기에 잔존하는 양을 의미하는 것으로도 해석할 수 있다. 이러한 잔존 자본에 t+1기의 자본재 가격을 곱한 값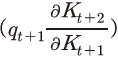 은 잔존 자본의 가치이며, 이를 t기 자본재의 가격(분모, )으로 나누면 자본을 보유함으로써 t+1기에 얻게 될 수익률로 볼 수 있다. 따라서 이상을 요약하면, 첫 번째 항(분모 포함)은 생산 측면의 수익률, 두 번째 항(분모 포함)은 보유가치3) 측면의 수익률로 경제적인 의미를 부여할 수 있다.
은 잔존 자본의 가치이며, 이를 t기 자본재의 가격(분모, )으로 나누면 자본을 보유함으로써 t+1기에 얻게 될 수익률로 볼 수 있다. 따라서 이상을 요약하면, 첫 번째 항(분모 포함)은 생산 측면의 수익률, 두 번째 항(분모 포함)은 보유가치3) 측면의 수익률로 경제적인 의미를 부여할 수 있다.
한편, 식 (1)에서 기업가치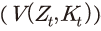 는 배당이 포함된 주가와 동일하며, 계속 가치
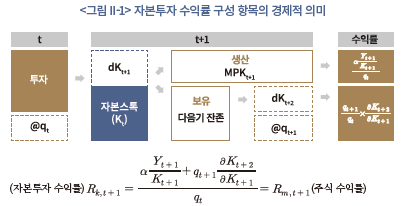
는 배당이 포함된 주가와 동일하며, 계속 가치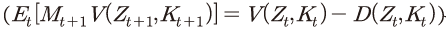 는 배당 후 주가에 해당한다. 이에 따라 t+1기의 배당 전 주가를 분자, t기의 배당 후 주가를 분모로 하여 t+1기의 주식 수익률
는 배당 후 주가에 해당한다. 이에 따라 t+1기의 배당 전 주가를 분자, t기의 배당 후 주가를 분모로 하여 t+1기의 주식 수익률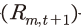 을 표현하면 식 (7)과 같다.
을 표현하면 식 (7)과 같다.
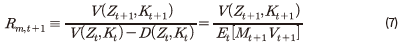
Restoy and Rockinger(1994)에 따르면, 동 모형에 적용된 가정 하에서 사후적인(ex-post) 자본투자 수익률과 주식 수익률 간에는 동일성이 성립한다.4) 이는 실물 부문과의 연관성에 기반하여 주식 수익률을 분석할 수 있는 실마리를 제공한다는 점에서 중요한 결과라 할 수 있다. 다음 장의 실증 분석도 두 수익률 간의 동일성을 이론적인 배경으로 하게 된다.
다만, 동 모형은 현실성의 측면에 있어서는 한계점이 존재한다. 2000년대 들어 국내 기업의 해외 생산기지가 상당히 확대되었기 때문에 이를 고려하여 실증 분석 모형을 구축하는 것이 이상적인 접근일 것이다. 하지만, 자료의 제약 등으로 인해 폐쇄 경제(closed economy)를 가정하여 모형을 구축했다는 점을 밝혀 둔다.
III. 실증 분석
본 장에서는 실증 분석 방법론에 관해 설명하고 자본투자 수익률의 추정 결과와 주요 특징에 대해 논의한다. 여기에서 실증 분석은 크게 두 부분으로 구성된다. 첫 번째는 자본투자 수익률 모형의 모수 추정 결과와 주식 수익률에 대한 자본투자 수익률의 설명력에 대한 평가이다. 이 부분에서는 이론적으로 구축된 모형이 주식 수익률의 장기 시계열을 설명하는 데 유용하게 활용될 수 있는지 확인해 보고자 한다. 두 번째는 자본투자 수익률의 구성 요소에 내재된 주요 특징에 대한 분석이다. 여기에서는 자본투자 수익률을 요인별로 분해하고, 각 요인의 시계열적 특징을 실물 경제 부문의 변화와 연관지어 고찰해 보고자 한다.
1. 방법론
실증 분석에서는 기본적으로 모형의 모수 추정과 해당 추정치를 이용한 자본투자 수익률의 산출이 필요하다. 추정 모형은 식 (5)와 자본투자 수익률과 주식 수익률 간 동일성을 이용하여 식 (8)과 같은 형태로 도출된다.
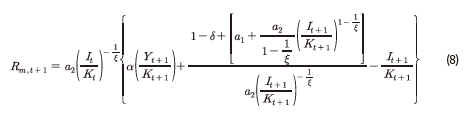
식 (8)에서 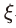 와
와 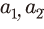 는 모두 자본축적식에 포함된 모수이다.
는 모두 자본축적식에 포함된 모수이다. 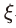 는 자본조정비용을 결정하는 핵심적인 모수이며,
는 자본조정비용을 결정하는 핵심적인 모수이며, 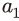 과
과 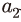 는
는 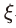 에 의존성을 가지는 모수로 Jermann(1998), Kaltenbrunner & Lochstoer(2010)에서와 같이 장기균형 조건5)을 적용하여 산출된다. 생산함수의 모수
에 의존성을 가지는 모수로 Jermann(1998), Kaltenbrunner & Lochstoer(2010)에서와 같이 장기균형 조건5)을 적용하여 산출된다. 생산함수의 모수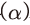 와 감가상각률
와 감가상각률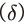 의 경우, 데이터 및 기존 문헌 등을 바탕으로 결정된다.6) 한편, 모형 내 각 변수의 시계열은 국민계정 자료와 주가 지수 등을 이용하여 구축되는데 관련 내용은 다음 절에서 별도로 설명하도록 하겠다.
의 경우, 데이터 및 기존 문헌 등을 바탕으로 결정된다.6) 한편, 모형 내 각 변수의 시계열은 국민계정 자료와 주가 지수 등을 이용하여 구축되는데 관련 내용은 다음 절에서 별도로 설명하도록 하겠다.
전술한 모수 중에서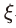 는 모형 설정과 관련하여 중요한 특징을 갖는다. 만약
는 모형 설정과 관련하여 중요한 특징을 갖는다. 만약 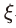 가 무한대에 가까워지면 자본조정비용은 0에 수렴하게 된다. 따라서
가 무한대에 가까워지면 자본조정비용은 0에 수렴하게 된다. 따라서 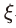 가 매우 큰 수치로 추정된다면 이는 모형 설정상 자본조정비용의 필요성을 기각하는 결과가 될 수 있다. 반면,
가 매우 큰 수치로 추정된다면 이는 모형 설정상 자본조정비용의 필요성을 기각하는 결과가 될 수 있다. 반면, 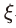 가 작은 양수값을 가진다면 모형에서 자본조정비용을 포함하는 것이 타당함을 뒷받침하는 결과가 될 것이다. 그리고
가 작은 양수값을 가진다면 모형에서 자본조정비용을 포함하는 것이 타당함을 뒷받침하는 결과가 될 것이다. 그리고 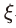 가 작은 양수일수록 자본조정비용이 증가하여 동일한 자본 대 투자 비율
가 작은 양수일수록 자본조정비용이 증가하여 동일한 자본 대 투자 비율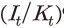 에 대해 추가로 축적되는 자본량이 감소하게 된다.7)
에 대해 추가로 축적되는 자본량이 감소하게 된다.7)
비선형성을 갖는 식 (8)은 별도의 변형 없이 최소자승법(Least Squares: LS) 및 일반화 적률법(Generalized Method of Moments: GMM)8)을 각각 적용하여 추정된다. 동 추정에서는 국소해(local optimum)나 불안정성 등의 문제를 피하기 위해 강건한 방식인 그리드 탐색법(grid search)을 적용하였다. 그리고 추정치의 표준오차는 500개의 표본을 이용한 부트스트랩(bootstrap) 방법에 따라 산출된다.
2. 데이터
실증 분석 모형(식 (8))을 추정하기 위해서는 주식 수익률과 식 (8)의 우변에 포함된 각 실물 경제 지표의 시계열 자료가 필요하다. 자료 구축에서 한 가지 유념했던 점은 식 (8)의 좌변에 있는 주식 수익률은 기본적으로 민간 부문만을 포괄하는 지표라는 것이다. 이 경우, 자본투자 수익률(우변)을 구성하는 실물지표에 정부 부문이 포함될 경우 일관성이 부족해지는 문제가 있을 수 있다. 따라서 우변에 속하는 실물지표는 모두 민간 부분을 대상으로 하여 자료를 구축하였다.
아울러, 민간 부문에 대한 집계 자료는 세부문의 가격 디플레이터와 물량지표(실질액)를 이용하여 합산(aggregation)했다는 점을 밝혀 둔다. 우리나라의 국민총생산 자료는 연쇄 라스파이레스(chained Laspeyres) 방식9)에 의해 작성되는데, 이 방식의 특성상 세분류 항목의 실질액을 단순 합산한 결과가 대분류의 실질액과 일치하지 않게 된다. 이러한 비가법성(non-additivity)을 고려하여 국민계정 편제시와 동일한 방법을 적용하여 민간 부문의 실질액을 구하였다. 세부적으로는, 민간 총생산의 경우 경제활동별 GDP에서 비정부 부문의 실질 생산액을 GDP 편제 방식에 따라 산출하여 사용하였다. 그리고 투자는 민간 부문의 투자 항목 중 주거용 건물 및 재고를 제외한 생산용 자본투자를 대상으로 하였다.10) 여기에는 비주거용 건물, 토목건설, 운송장비, 기계류, 연구개발, 기타 지식재산생산물이 포함된다. 자본 스톡은 공식 통계인 국민대차대조표 자료를 이용하였는데, 투자와 마찬가지로 생산용 자본(민간 부문)을 대상으로 하였다.11) 자본투자 수익률은 실질 개념이므로 주식 수익률은 KOSPI 지수를 소비자물가로 실질화한 자료를 사용하였다.
실증 분석의 대상 기간은 1980년부터 2021년까지이며 연간 자료를 바탕으로 추정된다. 자본 스톡의 공식 통계인 국민대차대조표가 연간 단위로 작성되기 때문에 자료의 주기는 이를 기준으로 하였다. 본 연구는 주식 및 자본투자 수익률의 중장기적인 흐름에 초점을 두고 있으므로, 저빈도의 자료를 사용하더라도 분석의 목적에서 크게 벗어나지 않을 것으로 판단된다.
3. 실증 분석 결과
여기에서는 전술한 방법론과 데이터를 통해 산출된 실증 분석 결과를 제시한다. 본 절의 전반부에서는 추정된 모수와 자본투자 수익률에 대해 살펴보고, 자본투자 수익률이 주식 수익률을 의미 있게 설명할 수 있음을 확인하도록 한다. 후반부에서는 자본투자 수익률 결정요인의 시계열적인 특징에 대하여 구조적 요인들의 변화와 연관지어 논의하고자 한다.
가. 모수 및 자본투자 수익률
<표 III-1>에는 최소자승법(LS)과 일반화 적률법(GMM)으로 추정한 자본조정비용의 모수(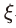 )가 제시되어 있다. 두 추정치는 각각 0.86(LS)과 0.87(GMM)로 매우 유사하고 모두 1% 수준에서 유의한 것으로 나타났다. 그리고 GMM 추정에서 J-통계량의 p-value는 0.24로 기본 조건인 결합 외생성(joint exogeneity)을 만족하는 것으로 분석된다. 두 방식으로 추정된
)가 제시되어 있다. 두 추정치는 각각 0.86(LS)과 0.87(GMM)로 매우 유사하고 모두 1% 수준에서 유의한 것으로 나타났다. 그리고 GMM 추정에서 J-통계량의 p-value는 0.24로 기본 조건인 결합 외생성(joint exogeneity)을 만족하는 것으로 분석된다. 두 방식으로 추정된 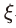 는 모두 자본조정비용이 존재하지 않는다는 조건
는 모두 자본조정비용이 존재하지 않는다는 조건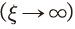 과는 상당한 차이12)가 있다. 따라서 자본조정비용이 기업의 의사결정에 유의미한 영향을 미친다는 점을 알 수 있다.
과는 상당한 차이12)가 있다. 따라서 자본조정비용이 기업의 의사결정에 유의미한 영향을 미친다는 점을 알 수 있다.

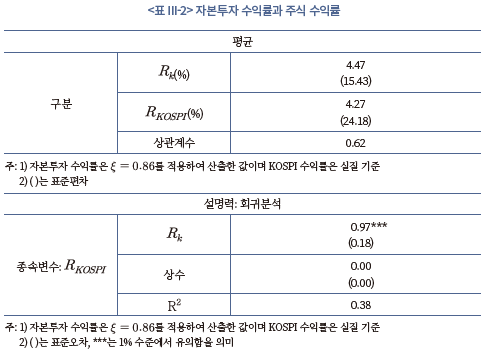
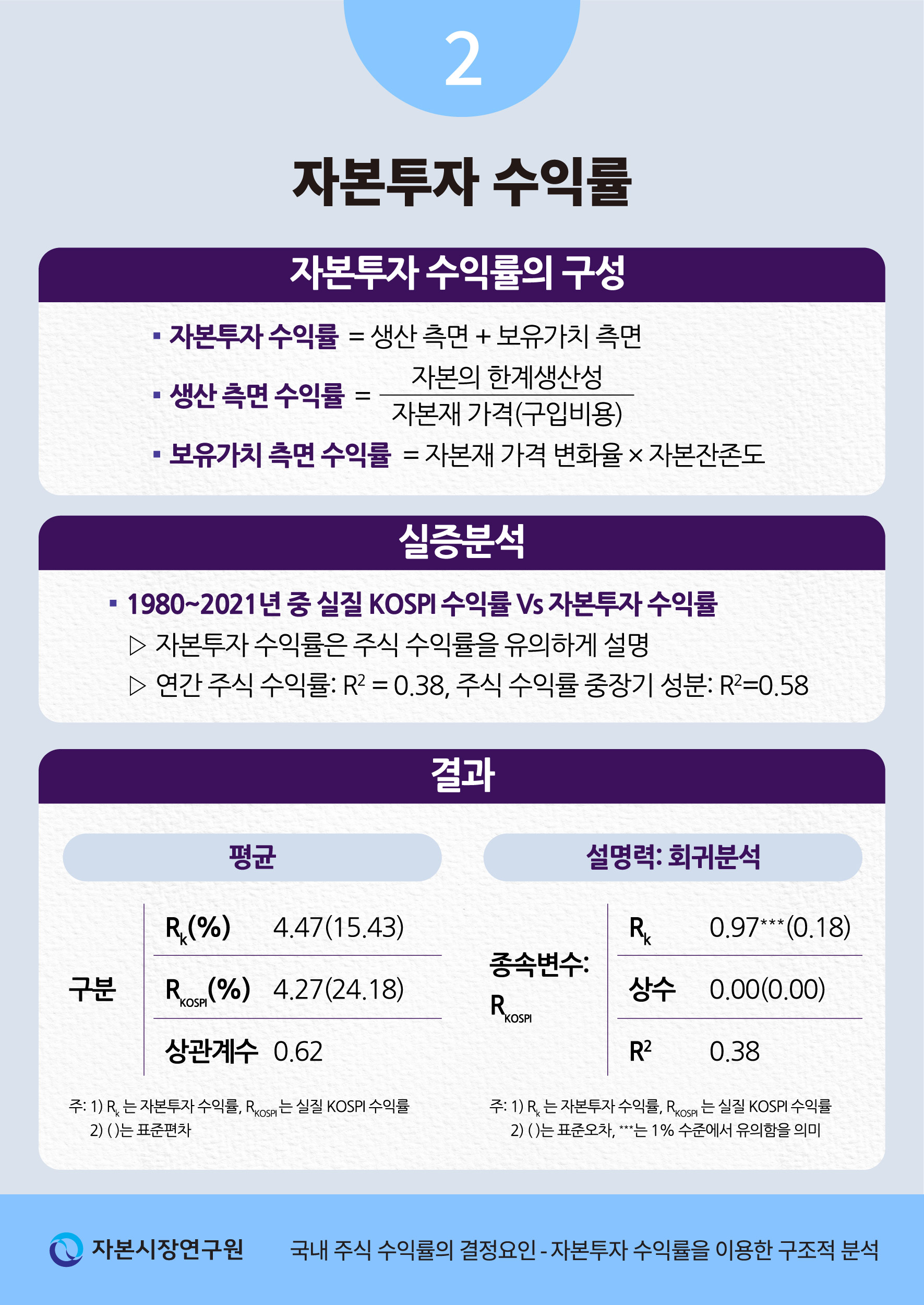
위와 같이 모수가 추정되면, 이를 바탕으로 각 시점의 자본투자 수익률을 산출하여 주식 수익률과 비교해 볼 수 있다. <표 III-2>의 상단에는 자본투자 수익률과 실질 KOSPI 수익률의 평균, 하단에는 자본투자 수익률의 실질 KOSPI 수익률에 대한 설명력을 분석한 결과가 제시되어 있다. 먼저 평균의 경우, 자본투자 수익률은 4.47%, 실질 KOSPI 수익률은 4.27%로 두 수익률 간에 큰 차이가 존재하지 않는다. 변동성의 경우, 자본투자 수익률(표준편차: 15.43%)이 상대적으로 완만하게 변화하여 KOSPI 수익률(표준편차: 24.18%)에 비해 다소 낮은 편이다. 하지만, 방향성 측면에서는 상당히 유사한 움직임을 보이면서 두 수익률은 0.62의 높은 상관계수를 나타낸다. 다음으로 하단의 회귀분석에 따르면, 자본투자 수익률의 계수는 1에 가깝고 1% 수준에서 유의한 것으로 나타났다. 그리고 회귀식의 결정계수(R2)는 0.38로 추정되어 자본투자 수익률의 설명력이 낮지 않은 것으로 평가된다.13)
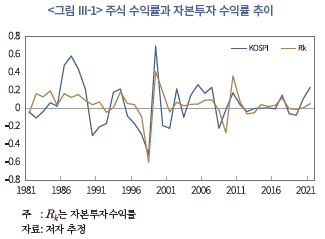
<그림 III-1>은 추정된 자본투자 수익률과 주식 수익률의 움직임을 명시적으로 나타내고 있다. 앞서 제시된 통계량이 의미하듯이, 자본투자 수익률은 주식 수익률에 비해 한층 완만하게 움직이지만, 두 수익률은 전반적으로 유사한 방향성을 가지고 있음을 확인할 수 있다. 이상의 결과는 단기적인 측면에서 주식 수익률이 기업의 실물 투자 활동과 그 성과에 어느 정도 연동되어 있다는 점을 시사한다.
주식 수익률이 실물 요인을 잘 반영한다면, 중장기적인 측면에서도 자본투자 수익률과 밀접한 연관성을 가질 것으로 예상할 수 있다. 이러한 점을 고려하여 자본투자 수익률과 주식 수익률의 5년 이동 평균과 중장기 성분을 이용하여 각각의 추이를 비교해 보았다. 여기에서 중장기 주기성분은 Christiano-Fitzgerald 필터를 이용하여 수익률의 2~5년 주기성분을 추출한 것이다.
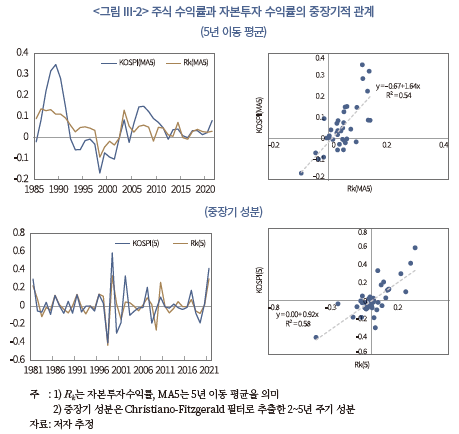
<그림 III-2>의 상단은 5년 이동 평균, 하단은 Christiano-Fitzgerald 필터로 추출한 중장기 성분을 각각 나타내고 있다. 이동 평균의 추이(<그림 III-2> 상단 좌측)를 보면, 1980년대 후반과 외환위기 및 글로벌 금융위기 전후에 주식 수익률의 변동성이 높기는 하지만, 이전보다는 자본투자 수익률에 한층 더 가까운 움직임을 보인다는 점을 알 수 있다.
그리고 이동 평균을 이용한 회귀식의 결정계수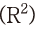 는 0.54로 자본투자 수익률의 설명력이 상당히 높은 것으로 분석되었다(<그림 III-2> 상단 우측). 아울러 두 수익률의 주기 성분(<그림 III-2> 하단)에서도 이와 유사한 결과를 확인할 수 있다. 즉, 두 주기 성분이 동조화된 움직임을 보이면서 자본투자 수익률의 주기 성분이 주식 수익률의 주기 성분을 상당 부분 설명하는 것으로 분석된다
는 0.54로 자본투자 수익률의 설명력이 상당히 높은 것으로 분석되었다(<그림 III-2> 상단 우측). 아울러 두 수익률의 주기 성분(<그림 III-2> 하단)에서도 이와 유사한 결과를 확인할 수 있다. 즉, 두 주기 성분이 동조화된 움직임을 보이면서 자본투자 수익률의 주기 성분이 주식 수익률의 주기 성분을 상당 부분 설명하는 것으로 분석된다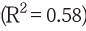 . 이러한 결과는 중장기적인 주가의 흐름을 이해하는 데 있어 자본투자 수익률이 유용하게 활용될 수 있음을 의미한다고 하겠다.
. 이러한 결과는 중장기적인 주가의 흐름을 이해하는 데 있어 자본투자 수익률이 유용하게 활용될 수 있음을 의미한다고 하겠다.
나. 주요 특징: 개관
앞 절의 결과에서 주식 수익률의 중장기적인 움직임을 설명하는 데 자본투자 수익률이 높은 설명력을 가진다는 점을 알 수 있었다. 본 절에서는 자본투자 수익률을 구성하는 각 요인들에 대해 보다 자세히 살펴보면서 주요 특징에 대해 논의하고자 한다. 여기에서는 먼저 전반적인 특징에 대해 개관하고, 세부적인 내용에 대해서는 다음 절에서 다루도록 하겠다.
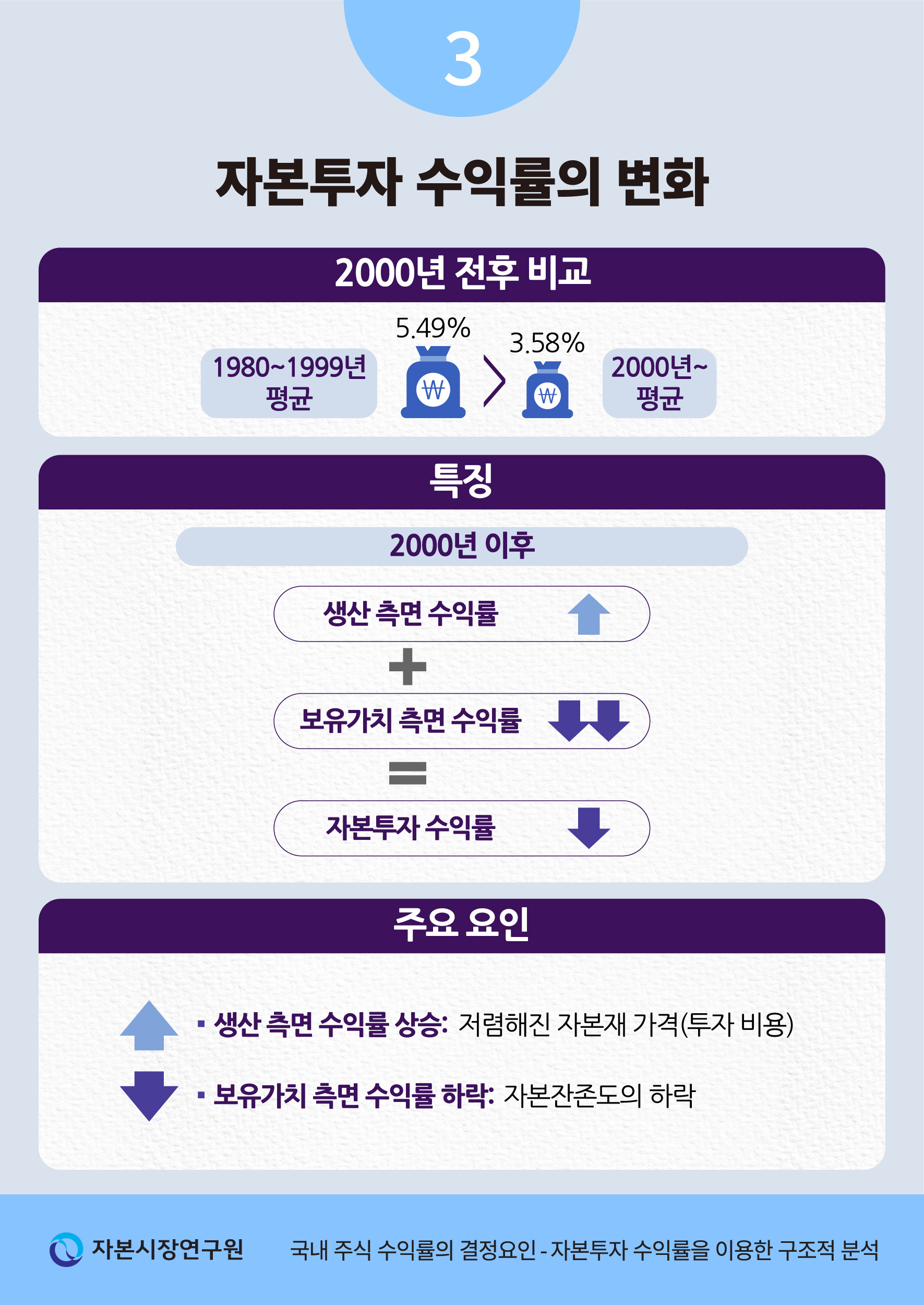
II장에서 언급했듯이 자본투자 수익률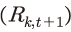 은 식 (6)과 같이 생산 측면과 보유가치 측면의 수익률로 나누어 볼 수 있다.14) <표 III-3>은 이러한 구분에 따라 2000년 전후 기간의 자본투자 수익률 평균과 그 차이를 생산과 보유가치 측면의 수익률로 나누어 제시하고 있다. 우선 (A)와 (B)열을 보면, 2000년 이후 자본투자 수익률은 3.58%로 이전(5.49%)에 비해 평균적으로 약 2%p 하락15)했다는 점이 나타난다. 이는 일차적으로, 1980~1990년대의 고도 성장기를 지나 저성장 국면으로 진입한 데 따른 결과로 풀이할 수도 있다. 하지만 식 (6)에 따라 각 구성 요소를 분해하면 다른 관점에서 자본투자 수익률의 변화에 대해 분석해 볼 수 있다.
은 식 (6)과 같이 생산 측면과 보유가치 측면의 수익률로 나누어 볼 수 있다.14) <표 III-3>은 이러한 구분에 따라 2000년 전후 기간의 자본투자 수익률 평균과 그 차이를 생산과 보유가치 측면의 수익률로 나누어 제시하고 있다. 우선 (A)와 (B)열을 보면, 2000년 이후 자본투자 수익률은 3.58%로 이전(5.49%)에 비해 평균적으로 약 2%p 하락15)했다는 점이 나타난다. 이는 일차적으로, 1980~1990년대의 고도 성장기를 지나 저성장 국면으로 진입한 데 따른 결과로 풀이할 수도 있다. 하지만 식 (6)에 따라 각 구성 요소를 분해하면 다른 관점에서 자본투자 수익률의 변화에 대해 분석해 볼 수 있다.
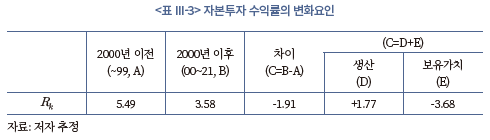
<표 III-3>의 (D)열과 (E)열을 보면 보유가치 측면의 수익률(-3.68%, E)은 전체 자본투자 수익률(-1.91%, C)과 같은 방향성을 가지고 하락하였지만, 생산 측면의 수익률(+1.77%, D)은 소폭 상승했다는 점이 나타난다. 즉, 보유가치 측면의 수익률이 크게 하락하면서 2000년 이후 자본투자 수익률이 전반적으로 낮아지기는 했지만, 생산 측면의 수익률은 오히려 자본투자 수익률을 높이는 요인으로 작용한 것이다. 아래에서는 두 요인이 이처럼 다른 방향성을 가지고 변화한 배경에 대해 분석하기 위해 생산과 보유가치 측면 수익률의 구성 요소를 보다 세분화하여 살펴보도록 하겠다.
다. 주요 특징: 생산 측면의 수익률
Ⅱ장에서 논의한 바와 같이 생산 측면의 수익률은 자본의 한계생산성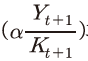 과 자본재의 가격
과 자본재의 가격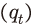 에 의해 결정된다. 특히, 식 (9)가 함축하는 바와 같이 다른 조건이 일정하다면, 자본의 한계생산성이 높거나 자본재의 가격이 낮을수록 생산 측면의 수익률은 증가하게 된다. 앞 절의 결과에 따르면 2000년 이후 생산 측면의 수익률은 이전에 비해 높아졌는데, 이는 언급한 두 가지 상승 요인이 모두 작용한 결과이거나 하나의 상승 요인이 더 큰 영향을 미친 데 따른 결과일 것이다.
에 의해 결정된다. 특히, 식 (9)가 함축하는 바와 같이 다른 조건이 일정하다면, 자본의 한계생산성이 높거나 자본재의 가격이 낮을수록 생산 측면의 수익률은 증가하게 된다. 앞 절의 결과에 따르면 2000년 이후 생산 측면의 수익률은 이전에 비해 높아졌는데, 이는 언급한 두 가지 상승 요인이 모두 작용한 결과이거나 하나의 상승 요인이 더 큰 영향을 미친 데 따른 결과일 것이다.
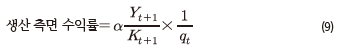
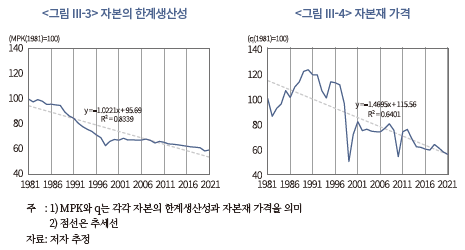
이러한 점을 염두에 두고 자본의 한계생산성(<그림 III-3>)과 자본재 가격(<그림 III-4>)의 추이를 살펴보면, 자본재 가격 하락이 생산 측면의 수익률을 상승시킨 요인이라는 점을 알 수 있다. <그림 III-3>에 따르면 자본의 한계생산성은 1980년대부터 현재까지 대체로 하락하는 추세를 나타내면서 생산 측면의 수익률을 낮추는 요인으로 작용하였다. 반면, <그림 III-4>에 나타난 자본재 가격의 경우, 1990년경부터 하락하는 모습을 보이면서 생산 측면의 수익률을 높이는 요인으로 작용했음을 알 수 있다. 그리고 전체적으로는 자본재 가격 하락이 자본의 한계생산성 하락에 의한 영향보다 크게 작용하여 2000년 이후 생산 측면의 수익률이 상승한 것으로 분석된다. 즉, 자본투입의 효율이 감소하기는 했지만, 자본을 보다 저렴한 비용으로 구입할 수 있게 됨으로써 생산 측면의 수익률이 높아졌다는 것을 의미한다.
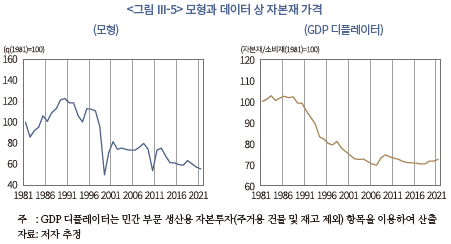
<그림 III-4>에 제시된 자본재 가격은 균형 모형에서 산출된 것으로, 이론적인 추정치에 해당한다. 하지만, 여기에도 현실적인 상황이 어느 정도 반영된 것으로 볼 수 있다. <그림 III-5>는 실제 데이터(GDP 디플레이터)를 통해 산출한 자본재의 가격16)을 나타내고 있는데, 동 계열은 모형의 추정치와 유사한 경향을 나타낸다. 추정된 자본재 가격(좌측)을 보면, 1990년대부터 하락 추세가 비교적 뚜렷해지는데, GDP 디플레이터(우측)로 산출된 자본재의 가격도 비슷한 시기부터 하락 추세를 보인다는 점을 확인할 수 있다. IMF(2019)에 따르면 1990년대부터 2010년대 중반까지 세계화의 진전과 국가별 생산 특화 및 경쟁 심화의 영향으로 전 세계적으로 자본재 가격이 하락하는 모습이 두드러진다. 이러한 점으로 비추어 볼 때, 글로벌 자본재 가격 하락의 영향이 국내 자본재 가격에도 일정 부분 작용했을 것으로 볼 수 있다. 아울러 국내적으로 제조업 중심의 산업 정책이 적극 추진되어 자본재 공급 능력이 확대된 데 따른 영향도 있었을 것으로 생각된다.
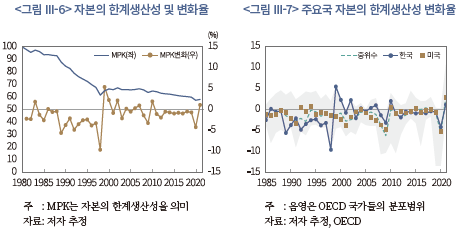
한편, 앞서 언급한 바와 같이 자본의 한계생산성은 하락세를 나타내면서 2021년의 한계생산성은 1980년 대비 60% 수준으로 낮아졌다. <그림 III-6>에서 자본의 한계생산성을 시기별로 보면, 특히 1980년대 중·후반부터 외환위기 발생 이전까지 가파른 하락세가 이어진 것이 관측된다. 이러한 점은 주요국과의 비교에서도 두드러지는 특징이라 할 수 있다. <그림 III-7>은 OECD 국가들을 대상(1985년부터 자료 존재)으로 하여 자본의 한계생산성 변화율17) 추이를 나타내고 있는데, 그림에서 음영은 분포 구간, 점선은 중위수를 표시하고 있다. 전반적인 추이를 통해 알 수 있듯이, 우리나라의 변화율은 대체로 외환위기 이전까지 음(-)일 뿐만 아니라 중위수보다 낮은 수준을 보였고, 이에 따라 자본의 한계생산성이 큰 하락폭을 나타냈다.
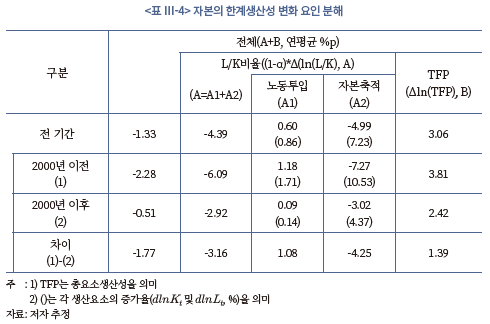
이상과 같이 1980~1990년대에 자본의 한계생산성이 크게 하락한 데에는 노동투입 및 총요소생산성(Total Factor Productivity: TFP) 증가에 비해 자본축적이 매우 빠르게 진행되었던 것이 주원인으로 작용하였다. 이는 기간별로 자본의 한계생산성 변화 요인을 분해한 <표 Ⅲ-4>를 통해 확인할 수 있다. <표 Ⅲ-4>에 따르면, 자본의 한계생산성은 전체 기간 중 연평균 1.33% 하락하였는데, 1980~1990년대에는 2.28% 하락하여 2000년 이후와는 약 -1.77%p의 격차가 존재한다. 1980~1990년대의 경우 노동투입 증가율(2000년 대비 기여도 격차: +1.08%p)과 TFP 증가율(2000년 대비 기여도 격차: +1.39%p)은 2000년 이후보다 더 높았다. 하지만 자본축적이 급속도로 진행된 결과(2000년 대비 기여도 격차: -4.25%p), 1980~1990년대에 자본의 한계생산성이 상대적으로 크게 하락한 것으로 평가된다. 이러한 결과를 종합하면, 2000년 전후 자본의 한계생산성 하락폭 차이를 결정하는 데 있어 자본축적 속도(2000년 이전: 10.53%, 이후: 4.37%)가 가장 큰 영향을 미쳤음을 알 수 있다. 다만, 두 기간의 하락폭 차이가 외환위기에 따른 대규모 조정이 2000년대 초에 일시적으로 집중된 데 따른 결과인지, 혹은 2000년대 들어 전반적으로 지속된 특징인지 여부에 대해 <표 Ⅲ-4>를 통해 알기는 어렵다. 이를 파악하기 위해서는 시계열을 통해 변동 상황을 확인할 필요가 있을 것이다.
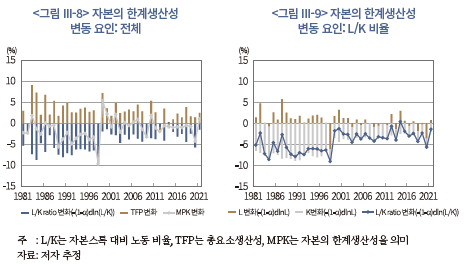
이에 따라 <그림 III-8> 및 <그림 III-9>와 같이 자본의 한계생산성 변동 요인별로 기여도를 구분하여 시계열을 나타내 보았다. <그림 III-8>에 따르면 총요소생산성은 대체로 자본의 한계생산성을 증가시키는 요인으로 작용하고 있지만 기여도는 대체로 축소되는 모습이 관측된다. L/K 비율 변화는 자본의 한계생산성을 하락시키는 요인이었지만 외환위기 이후 그 영향(절대값)이 전반적으로 축소된 특징이 있다. 그리고 <그림 III-9>를 보면, 자본축적에 따른 음(-)의 기여도는 외환위기 직후 그 절대 수준이 크게 감소한 후 외환위기 이전에 비해 작은 수준(절대값)을 계속 유지하고 있다. 이러한 결과는 외환위기에 따른 일시적인 조정이 아니라, 구조적인 자본축적 감속이 지속되면서 자본생산성의 하락폭이 전반적으로 축소되었음을 의미한다. 아울러 <그림 III-9>는 2000년 전후 노동투입(2000년 이전 증가율: 1.17%, 이후: 0.14%)이 자본의 한계생산성에 미치는 영향도 변화했음을 보여준다. 외환위기 기간을 제외하면 노동투입은 2000년까지 자본의 한계생산성 하락을 부분적으로 상쇄하는 요인이었다. 하지만 이후에는 대체로 0에 가까운 기여도를 보이면서 자본의 한계생산성 변화에 중립적으로 작용한 것으로 나타난다.
앞서 언급했듯이 2000년 이후 총요소생산성이 자본의 한계생산성 변화에 미친 양(+)의 기여도는 이전 기간에 비해 줄어든 경향이 있다. <그림 III-10>에 제시된 장기 시계열을 보면, 총요소생산성 증가율은 대체로 둔화되는 모습을 보이는 가운데 최근에는 2% 내외의 수준을 나타내고 있다. 총요소생산성 증가율은 기술 진보 정도를 포착하는 주요 지표이므로 이와 같은 흐름은 성장잠재력이 축소되고 있음을 의미할 수 있다. 다소 우려되는 상황이라는 점은 분명하지만, 총요소생산성 증가율의 둔화는 비단 우리나라뿐만 아니라 주요국들도 경험하고 있는 현상으로 생각된다. <그림 III-11>은 1985년 이후 OECD 국가들의 총요소생산성 증가율18)을 표시하고 있는데, 이 국가들도 전반적으로 둔화되는 모습19)을 보이면서 우리나라와 유사한 양상을 나타낸다.
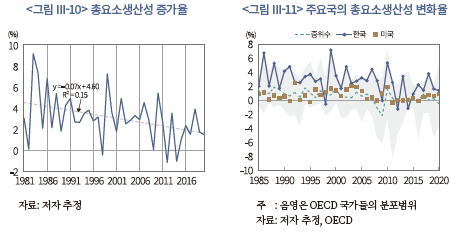
이 그림에서 한 가지 특기할 만한 사항으로 우리나라의 총요소생산성 변화율의 상대적인 크기에 주목해 볼 필요가 있다. 둔화되는 모습을 보이고는 있지만, 우리나라의 총요소생산성 증가율은 국가별 분포(음영)의 주로 상단에 위치하면서 상대적으로 높은 수준을 유지해 왔다. 즉, 과거 고도 성장기뿐만 아니라 최근까지도 이러한 경향을 이어가면서 미국을 비롯한 주요 선진국에 비해 높은 총요소생산성 증가율을 보였다는 점이 특징적으로 나타난다.
라. 주요 특징: 보유가치 측면의 수익률
보유가치 측면의 수익률은 식 (10)과 같이 자본재의 가격변화율인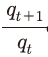 에 자본의 잔존도20)인
에 자본의 잔존도20)인 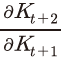 를 곱한 것으로, 다음 기에도 남게 될 자본을 t+1기의 시장가격으로 판매하는 경우를 가정한 수익률로 생각할 수 있다.
를 곱한 것으로, 다음 기에도 남게 될 자본을 t+1기의 시장가격으로 판매하는 경우를 가정한 수익률로 생각할 수 있다.
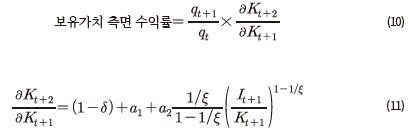
자본의 잔존도는 식 (11)과 같이 풀어 쓸 수 있는데, 이 식은 자본 잔존도가 감가상각률과 자본 대비 투자 비율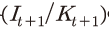 에 의해 결정됨을 의미한다. 만약 자본조정비용이 존재하지 않는다면 식 (11)이 상수21)로 단순화된다. 하지만, 그렇지 않은 경우에는
에 의해 결정됨을 의미한다. 만약 자본조정비용이 존재하지 않는다면 식 (11)이 상수21)로 단순화된다. 하지만, 그렇지 않은 경우에는 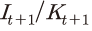 비율이 높을수록 잔존 자본이 커지게 되는데22), 이는 두 가지 의로 해석될 수 있다. 먼저, 신규투자가 기존에 축적된 자본과 같은 비율로 증가해야 잔존 자본이 동일하게 유지된다는 점을 의미한다. 다른 한편으로는, t+1기에 동일한 크기의 투자
비율이 높을수록 잔존 자본이 커지게 되는데22), 이는 두 가지 의로 해석될 수 있다. 먼저, 신규투자가 기존에 축적된 자본과 같은 비율로 증가해야 잔존 자본이 동일하게 유지된다는 점을 의미한다. 다른 한편으로는, t+1기에 동일한 크기의 투자 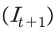 를 할지라도 기존에 설치된 자본 규모
를 할지라도 기존에 설치된 자본 규모 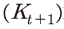 가 크다면, t+2기에 추가로 축적되는 자본이 축소되는 것으로 해석될 수도 있다. 즉, 자본축적 이후에 후속 투자가 충분하게 이루어지지 않으면 유효 자본의 증가에 제약이 따르는 것을 의미한다고 하겠다.
가 크다면, t+2기에 추가로 축적되는 자본이 축소되는 것으로 해석될 수도 있다. 즉, 자본축적 이후에 후속 투자가 충분하게 이루어지지 않으면 유효 자본의 증가에 제약이 따르는 것을 의미한다고 하겠다.
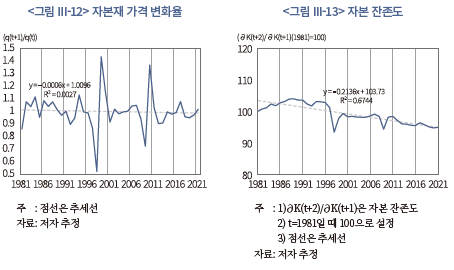
<그림 III-12>과 <그림 III-13>은 보유가치 측면의 수익률을 구성하는 요소인 자본재의 가격 변화율과 자본 잔존도의 시계열을 각각 나타내고 있다. 앞의 <그림 III-4>에서 자본재의 가격(수준)은 1990년 이후 대체로 하락하는 모습을 보였는데, <그림 III-12>에 제시된 자본재 가격의 변화율은 평탄한 형태를 띤다. 즉, 자본재 가격에는 하락 추세가 존재하지만 자본재 가격의 변화율에는 유의한 추세가 관측되지 않는다. 이는 자본재 가격이 하락하기는 했지만 그 하락세가 가속화되지 않았고, 따라서 자본재 가격의 변화율이 수익률을 평균적으로 크게 변화시키지는 않았음을 의미한다. 반면, <그림 III-13>에서 확인할 수 있는 것처럼 자본 잔존도에서는 하락 추세가 뚜렷하게 나타난다. 특히, 1990년 이후 자본 잔존도를 보면, 외환위기 당시 크게 낮아진 후 일시적으로 반등하기도 했지만 전반적으로는 하락세를 보인다. 따라서 외환위기를 계기로 자본 잔존도 감소가 본격적으로 진행되면서 보유가치 측면의 수익률에 하방 요인으로 크게 작용했음을 알 수 있다.23)
앞서 식 (11)을 바탕으로 논의한 바와 같이, 모형에 따르면 투자가 자본과 동일한 변화율로 증가해야 자본 잔존도가 일정하게 유지된다. 이를 바탕으로 생각할 때, 국내 자본 잔존도가 감소한 것은 지속적인 투자를 통해 이를 유지하는 데 한계가 따랐기 때문으로 판단된다. 1990년대 중반까지는 대기업을 중심으로 투자가 빠르게 확대되었지만, 외환위기 이후의 대규모 구조조정, 성장잠재력 하락 등으로 인해 기업들이 이전처럼 적극적으로 투자를 확대하기가 어려워졌을 것이다. 또한, <표 Ⅲ-4>와 <그림 III-9>에서 살펴본 것처럼 노동 공급의 정체로 인한 영향도 있을 것으로 판단된다. 즉, 자본의 한계생산성은 추가적인 노동 투입을 통해 개선될 수 있지만, 이를 확대할 수 있는 여력이 축소되면서 투자를 제약한 측면도 간과할 수 없을 것으로 생각된다.
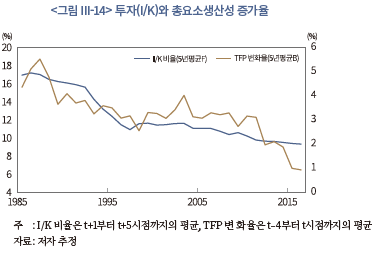
여기에서 성장잠재력 측면에서의 제약은 <그림 III-14>에 나타난 총요소생산성(TFP) 증가율과 자본 대비 투자 비율(I/K)의 관계를 통해 추론해 볼 수 있다. 그림에 표시된 TFP 증가율은 과거 t-4부터 t시점까지 5년간의 TFP 증가율 평균, I/K 비율은 미래 t+1부터 t+5시점까지 5년간의 I/K 비율 평균이다. 여기에서 두 계열은 밀접한 양의 상관관계를 가지면서 과거의 TFP 증가율이 미래의 I/K 비율을 유의하게 예측하는 것으로 분석된다.24) 이러한 점으로 볼 때, 투자가 둔화되면서 자본 잔존도가 하락한 데에는 TFP 증가율 둔화로 성장잠재력이 축소된 것이 일정 부분 영향을 미쳤을 것으로 생각된다.
IV. 시나리오 분석
III장에서는 자본투자 수익률이 주식 수익률의 중장기적인 흐름을 상당 부분 설명할 수 있다는 점을 실증적으로 확인할 수 있었다. 또한, 분석 결과에 따르면 자본투자 수익률은 보유가치 측면의 수익률 하락이 큰 영향을 미치면서 2000년대 들어 평균적으로 하락한 것으로 나타났다. 그리고 이러한 보유가치 측면의 수익률 하락에는 총요소생산성 증가율 하락과 노동 공급 정체 등이 투자를 제약함으로써 자본 잔존도가 낮아진 것이 원인으로 작용했다고 판단된다.
향후에도 자본투자 수익률은 기술 진보나 노동자원의 가용도에 따라 크게 달라질 수 있다. 따라서 본 장에서는 이러한 경제환경 변화에 대한 시나리오를 바탕으로 국내 자본투자 수익률을 전망하고 그 결과에 대해 논의하고자 한다. 특히, 인구 감소와 고령화는 현재 예상되는 가장 중요한 환경 변화로 노동부존량에 직접적인 영향을 미치는 만큼, 이와 관련된 시나리오에 초점을 맞추고자 한다. 여기에서는 방법론에 대해 먼저 간략히 설명한 다음, 시나리오 분석 결과를 제시하도록 하겠다.
1. 방법론
시나리오 분석은 외생변수인 노동부존량과 총요소생산성의 전제치를 바탕으로 내생변수들의 균형값을 산출하는 방식을 이용한다. 기업의 투자와 자본투자 수익률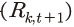 은 상기 외생변수의 움직임에 따라 결정되는 내생변수에 해당한다. 여기에서
은 상기 외생변수의 움직임에 따라 결정되는 내생변수에 해당한다. 여기에서 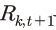 은 III장에서 설명한 대로 식 (12)와 같이 표현될 수 있다.
은 III장에서 설명한 대로 식 (12)와 같이 표현될 수 있다.
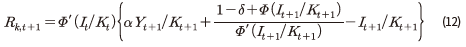
만약, 위의 식에서 t기의 투자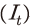 와 자본량
와 자본량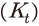 이 주어진다면, 자본축적식에 의해 t+1기의 자본량
이 주어진다면, 자본축적식에 의해 t+1기의 자본량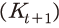 이 결정될 수 있다. 또한 외생적으로 주어진 노동부존량
이 결정될 수 있다. 또한 외생적으로 주어진 노동부존량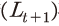 과 총요소생산성
과 총요소생산성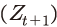 을 이용하면 t+1기의 생산량
을 이용하면 t+1기의 생산량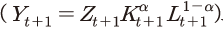 도 계산될 수 있다. 그러면 식 (12)에서 t+1기의 투자
도 계산될 수 있다. 그러면 식 (12)에서 t+1기의 투자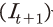 를 제외한 여타 변수는 모두 그 값이 결정되는데, 이때
를 제외한 여타 변수는 모두 그 값이 결정되는데, 이때 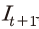 은 최적화 조건인 투자에 대한 오일러 방정식을 이용하여 산출될 수 있다.25)
은 최적화 조건인 투자에 대한 오일러 방정식을 이용하여 산출될 수 있다.25)

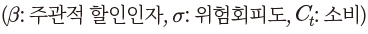
비확률적 균형에서 오일러 방정식은 식 (13)과 같이 정리되는데, 최적 투자는 이 방정식이 성립하는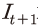 가 된다. 수치적으로는 식 (14)와 같이 정의된 목적함수를 최소화하는 값에 해당하며 그 해는 그리드 탐색을 통해 산출된다.26)
가 된다. 수치적으로는 식 (14)와 같이 정의된 목적함수를 최소화하는 값에 해당하며 그 해는 그리드 탐색을 통해 산출된다.26)
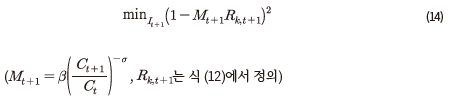
전술한 과정을 통해 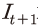 이 주어지면, t+2기의 자본량이 결정되게 된다. 그러면 위와 같은 일련의 연산 과정을 동일하게 반복하여 나머지 변수들의 t+2기 값을 산출할 수 있다. 이러한 과정을 순차적으로 적용하여 20년간의 시계열을 생성하면 주어진 시나리오에 대한 전망이 완료된다.27)
이 주어지면, t+2기의 자본량이 결정되게 된다. 그러면 위와 같은 일련의 연산 과정을 동일하게 반복하여 나머지 변수들의 t+2기 값을 산출할 수 있다. 이러한 과정을 순차적으로 적용하여 20년간의 시계열을 생성하면 주어진 시나리오에 대한 전망이 완료된다.27)
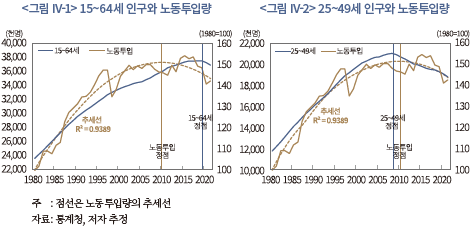
각 변수의 전망치를 산출하기 위한 실제 연산에서는 모형 내 모수값들과 함께 노동부존량과 총요소생산성에 대한 전제치가 필요하다. 노동부존량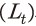 의 경우, 통계청 전망(2021년 발표 장래인구추계)에서의 인구증가율을 따라 변화하는 것으로 가정하였다. 단, 여기에서는 생산가능인구 연령대 전체를 포함하는 15~64세 대신 25~49세 인구의 증가율을 이용하였다. 이는 <그림 IV-1>과 <그림 IV-2>의 비교를 통해 알 수 있는 것처럼 25~49세 인구가 실제 노동투입량(민간 부문 종사자수×근로시간)을 보다 잘 포착하는 것으로 판단되기 때문이다. <그림 IV-1>을 보면, 15~64세 인구와 노동투입량이 실선, 그리고 노동투입량의 추세가 점선으로 표시되어 있다. 그림에 따르면 추세적인 노동투입량28)은 2010년경 정점에 도달한 것으로 보인다. 그런데 15~64세 인구의 경우 2019년경 정점에 도달한 것으로 나타나, 노동투입량의 추세적인 정점과는 시기적으로 큰 격차가 존재한다. 반면, <그림 IV-2>에 제시된 25~49세 인구를 보면, 동 인구의 정점은 2008년경으로 노동투입량 추세의 정점 도달 시기와 상당히 가까운 편이다. 해당 연령대는 노동시간이 적거나 비경제활동인구가 많은 미성년자, 은퇴 근접 및 은퇴 연령자들을 포함하지 않기 때문에 실제 추세를 잘 포착하는 것으로 생각된다.
의 경우, 통계청 전망(2021년 발표 장래인구추계)에서의 인구증가율을 따라 변화하는 것으로 가정하였다. 단, 여기에서는 생산가능인구 연령대 전체를 포함하는 15~64세 대신 25~49세 인구의 증가율을 이용하였다. 이는 <그림 IV-1>과 <그림 IV-2>의 비교를 통해 알 수 있는 것처럼 25~49세 인구가 실제 노동투입량(민간 부문 종사자수×근로시간)을 보다 잘 포착하는 것으로 판단되기 때문이다. <그림 IV-1>을 보면, 15~64세 인구와 노동투입량이 실선, 그리고 노동투입량의 추세가 점선으로 표시되어 있다. 그림에 따르면 추세적인 노동투입량28)은 2010년경 정점에 도달한 것으로 보인다. 그런데 15~64세 인구의 경우 2019년경 정점에 도달한 것으로 나타나, 노동투입량의 추세적인 정점과는 시기적으로 큰 격차가 존재한다. 반면, <그림 IV-2>에 제시된 25~49세 인구를 보면, 동 인구의 정점은 2008년경으로 노동투입량 추세의 정점 도달 시기와 상당히 가까운 편이다. 해당 연령대는 노동시간이 적거나 비경제활동인구가 많은 미성년자, 은퇴 근접 및 은퇴 연령자들을 포함하지 않기 때문에 실제 추세를 잘 포착하는 것으로 생각된다.
한편, 총요소생산성은 2010년 이후의 자료를 반영하여 해당 기간 중 증가율 평균(1.7%)에 따라 변화하는 것으로 가정하였다. 그리고 확률적 할인인자에 포함된 주관적 할인인자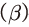 는 2010년 이후 무위험이자율29)을 바탕으로 0.998로, 위험회피도
는 2010년 이후 무위험이자율29)을 바탕으로 0.998로, 위험회피도 는 같은 기간에 대한 추정치30)를 이용하여 2로 설정하였다. 그리고 자본조정비용 함수에 포함된 모수값으로는 Ⅲ장의 추정치가 이용된다. 다만, 이상의 모수들은 모형 설정과 가계의 선호 및 기술의 변화 등에 따라 달라질 수 있음을 밝혀 둔다.
는 같은 기간에 대한 추정치30)를 이용하여 2로 설정하였다. 그리고 자본조정비용 함수에 포함된 모수값으로는 Ⅲ장의 추정치가 이용된다. 다만, 이상의 모수들은 모형 설정과 가계의 선호 및 기술의 변화 등에 따라 달라질 수 있음을 밝혀 둔다.
2. 시나리오 분석 결과
시나리오 분석에서는 통계청의 중위 인구 전망을 기본 시나리오로 하여 향후 20년간의 자본투자 수익률을 전망한다. 다만, 인구·노동정책, 기술 발전의 전개 양상 등에 따라 경제환경이 유동적으로 변화할 수 있기 때문에 기본 시나리오는 상당히 제한된 측면만을 조명한 것일 수 있다. 이러한 점을 고려하여 인구 전반, 고연령 인구의 노동시장 참여, 여성의 노동시장 참여, 총요소생산성 증가율에 대한 시나리오를 추가로 적용하여 전망치를 산출하고 결과를 비교하도록 하겠다. 이를 통해 여러 환경 변화가 자본투자 수익률에 미치는 영향에 대해 보다 종합적인 시각에서 평가해 볼 수 있을 것으로 생각된다.
가. 인구 시나리오
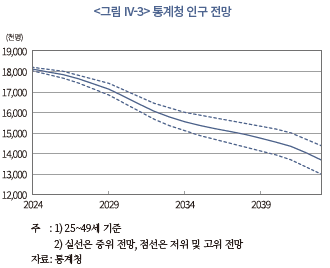
통계청의 장래 인구추계에서는 가정에 따라 저위, 중위, 고위 경로의 인구가 전망되어 있다. 전망 경로별로 수준의 차이는 있지만, 저출산의 장기화로 인해 우리나라의 인구가 당분간 감소할 것으로 예측된다는 점은 공통적이다. <그림 IV-3>은 세 종류의 전망치를 나타내고 있는데, 좌측 그림에서 실선은 중위 전망에 따른 25~49세 인구, 위와 아래의 점선은 각각 고위 및 저위 전망에 따른 동 연령의 인구에 해당한다. 이 중 중위 전망에 따르면, 2043년의 25~49세 인구는 약 1,370만명으로 2024년 대비 24% 감소하게 된다. 그리고 고위와 저위 전망에 따른 2043년의 인구는 중위 전망과 약 ±70만명의 차이를 보인다(<그림 IV-3> 우측). 전체 시계열을 보면 고위 및 저위 전망은 대체로 중위 전망을 중심으로 하여 대칭적인 모습을 보인다.
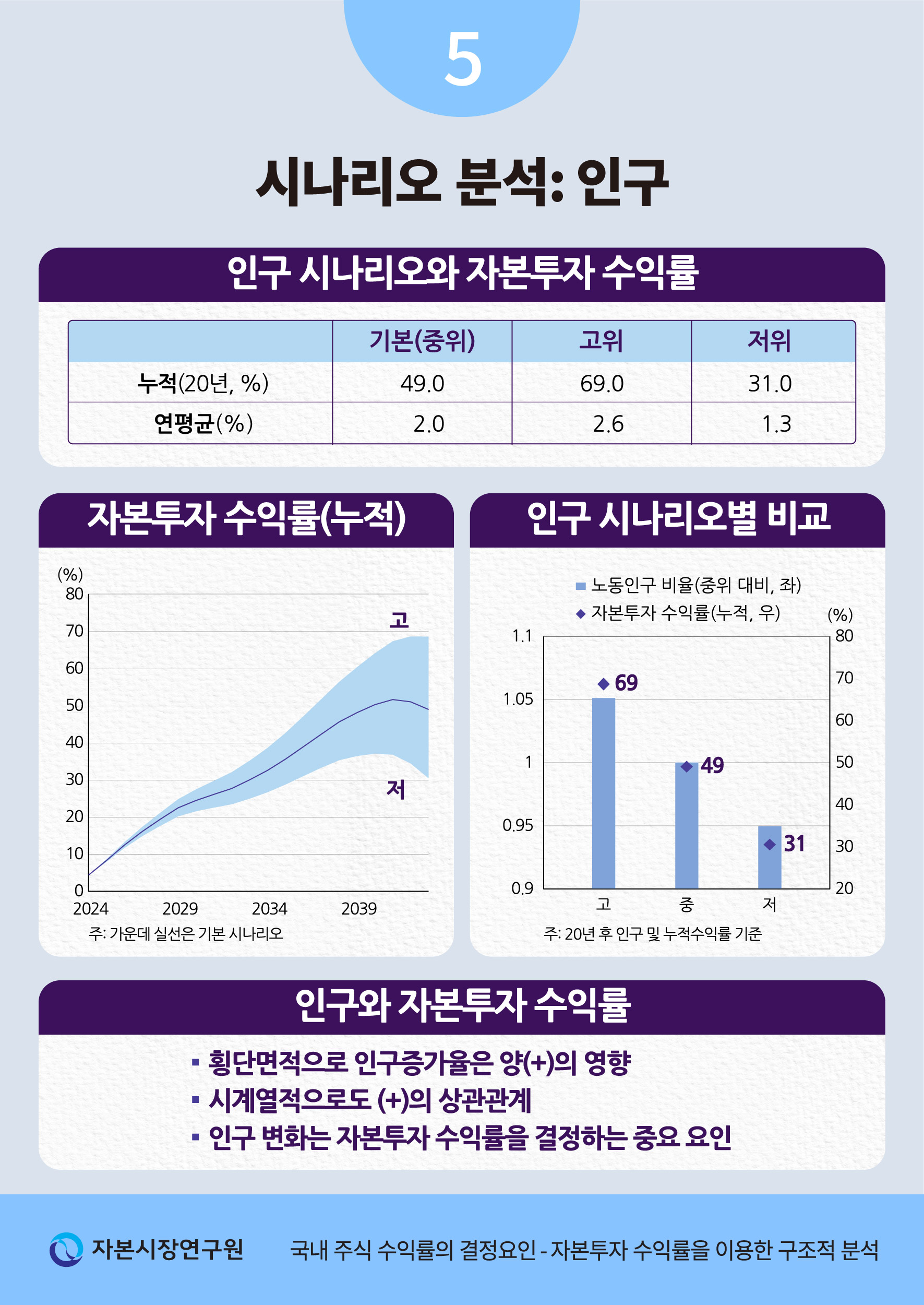
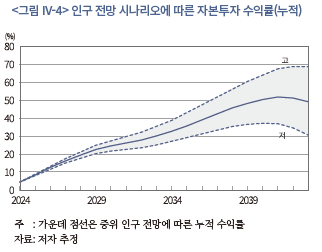
시나리오 분석에서는 노동투입량 증가율이 인구 증가율을 따르는 것으로 가정하여 상기 인구 전망을 각각 적용하였다. <그림 IV-4>는 세 개의 시나리오에서 산출된 자본투자 수익률(누적)을 제시하고 있다. 그림에서 가운데 실선은 중위 인구 시나리오, 위와 아래의 점선은 각각 고위 및 저위 인구 시나리오에 따른 누적수익률을 의미한다. 그리고 음영은 고위 및 저위 사이의 인구에서 산출되는 누적수익률에 해당한다. 먼저 중위 인구 시나리오에 따르면, 향후 20년간 누적수익률(실질, 이하 동일)은 약 49%로 전망되는데 연평균으로는 약 2.0%로 환산된다. 그리고 고위 인구 시나리오의 누적수익률은 약 69%(연평균 약 2.6%), 저위 인구 시나리오의 누적수익률은 약 31%(연평균 약 1.3%)로 산출된다.
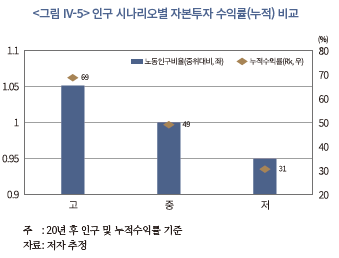
<그림 IV-5>는 이상의 결과를 종합하여 20년 후 인구 시나리오별 자본투자 수익률(누적, 점)과 중위 인구대비 비율(막대)을 표시하고 있다. 제시된 바와 같이 고위, 중위, 저위 수익률은 단계별로 20%p 내외의 격차를 보이면서 인구 규모가 클수록 높아지는 경향을 나타낸다. 앞서 언급한 바와 같이 중위 전망 대비 고위와 저위 인구는 약 5%의 차이를 보이는데, 누적수익률은 인구 격차(비율)의 4배에 가까운 차이가 존재한다. 이러한 결과는 향후 인구 변화가 자본투자 수익률을 결정하는 중요 요인이며, 인구 감소가 심화될수록 자본투자 수익률에 미치는 부정적인 영향이 커질 수 있다는 점을 시사한다.
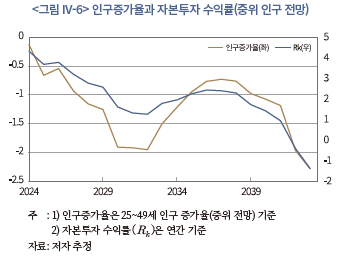
자본투자 수익률과 인구 변화의 밀접한 연관성은 누적수익률에 대한 횡단면 비교에서뿐만 아니라 연간 수익률의 시계열을 통해서도 확인된다. <그림 IV-6>은 연도별 평균 인구증가율 및 자본투자 수익률의 추이를 나타내고 있다. 25~49세 인구는 2024년부터 2030년 초, 2030년 말 이후 하락폭이 커지는데, 자본투자 수익률도 인구증가율과 유사한 움직임을 나타내면서 변화한다. 즉, 인구 감소가 심화되는 기간에 자본투자 수익률도 낮아지는 경향을 보인다.
지금까지는 인구 시나리오별 자본투자 수익률에 대해 전반적으로 비교해 보았다. 다음에서는 결정요인을 세분화하여 주요 특징에 대해 살펴보도록 하겠다. <그림 IV-7>은 자본투자 수익률의 변화 요인(2024년 대비)을 생산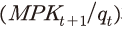 과 보유가치
과 보유가치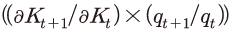 측면으로 나누어 표시하고 있다. 제시된 결과에 따르면, 자본투자 수익률은 2000년 이후와 유사한 특징을 가지고 변화할 것으로 예상된다. 실증 분석 결과를 보면, 2000~2021년 중에는 생산 측면의 양(+)의 영향보다는 보유가치 측면의 음(-)의 영향이 더 크게 작용한 것으로 추정되었다. <그림 IV-7>은 전망에서도 생산 측면의 수익률은 대체로 자본투자 수익률을 높이는 방향으로 작용하지만, 보유가치 측면의 수익률은 이를 낮추는 방향으로 작용함을 나타낸다. 그리고 결과적으로는 보유가치 측면의 하방 영향이 전반적으로 크게 작용하면서 자본투자 수익률이 낮아지는 모습을 보인다. 이러한 점을 볼 때, 향후에도 실증 분석에서 나타났던 경향이 당분간 지속될 것으로 예상할 수 있다.
측면으로 나누어 표시하고 있다. 제시된 결과에 따르면, 자본투자 수익률은 2000년 이후와 유사한 특징을 가지고 변화할 것으로 예상된다. 실증 분석 결과를 보면, 2000~2021년 중에는 생산 측면의 양(+)의 영향보다는 보유가치 측면의 음(-)의 영향이 더 크게 작용한 것으로 추정되었다. <그림 IV-7>은 전망에서도 생산 측면의 수익률은 대체로 자본투자 수익률을 높이는 방향으로 작용하지만, 보유가치 측면의 수익률은 이를 낮추는 방향으로 작용함을 나타낸다. 그리고 결과적으로는 보유가치 측면의 하방 영향이 전반적으로 크게 작용하면서 자본투자 수익률이 낮아지는 모습을 보인다. 이러한 점을 볼 때, 향후에도 실증 분석에서 나타났던 경향이 당분간 지속될 것으로 예상할 수 있다.
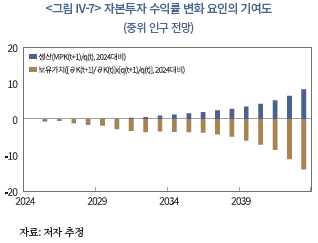
이러한 생산과 보유가치 측면에서의 변화는 III장 3절의 다 및 라 소절에서와 같이 한 단계 더 세분화된 수준에서 분석될 수 있다. 즉, 생산 측면은 자본재 가격과 자본의 한계생산성, 그리고 보유가치 측면은 자본재의 가격 변화율과 자본의 잔존도로 구분하여 살펴볼 수 있다. 먼저, <그림 IV-8>의 좌측은 생산 측면의 구성 요소를 나타내고 있다. 여기에서 자본의 한계생산성의 변화는 크지 않지만 자본재 가격 하락은 비교적 뚜렷하게 나타난다. 따라서 자본재 가격(하락)이 생산 측면의 수익률을 높이는 데 큰 영향을 주는 것으로 보인다. 이와 같은 자본재 가격의 하락세는 생산 측면의 수익률을 세분화했을 때 관측된 결과와 유사한 모습이다. 다음으로 <그림 IV-8>의 우측은 보유가치 측면의 요인을 나타내고 있는데, 여기에서는 자본재 가격 변화율과 자본의 잔존도가 모두 하락하는 모습을 보인다. 특히 자본재의 가격 변화율을 보면, 과거에는 뚜렷한 추세가 나타나지 않았지만, 향후에는 자본재 가격뿐만 아니라 자본재 가격 변화율도 하락하는 것으로 전망된다. 이는 인구 감소 심화로 인해 자본재 투자 수요가 충분히 뒷받침되지 않는 데 따른 결과로 생각할 수 있다.
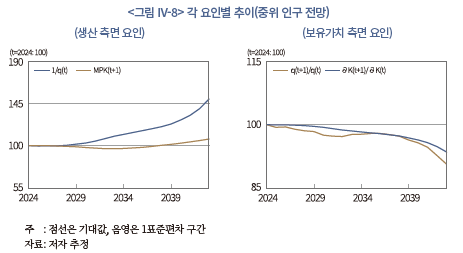
이상에서는 기본 전망에 초점을 맞추어 개별 결정요인의 시계열적인 특징에 대해 살펴보았다. 유사한 방법을 이용하면 각 인구 시나리오의 결과에 대해서도 결정요인별로 특징을 분석해 볼 수 있다. 그래서 여기에서는 앞서 고위, 중위, 저위 인구 시나리오에서 산출된 자본투자 수익률을 각 결정요인별로 세분화하여 시나리오 간 차이에 대해 논의하도록 하겠다.
<그림 IV-9>는 연간 자본투자 수익률을 생산 및 보유가치 측면의 요인으로 구분하여 중위 전망 대비 격차를 나타내고 있다. 먼저, 생산 측면의 수익률을 보면, 고위와 중위의 차이(고-중)는 대부분 음(-), 저위와 중위의 차이(저-중)는 대부분 양(+)의 수치를 보이면서 저위, 중위, 고위의 순으로 높다는 점을 알 수 있다. 다음으로 보유가치 측면의 경우, 고위와 중위의 차이(고-중)는 대부분 양(+), 저위와 중위의 차이는 대부분 음(-)의 수치로 고위 전망에서 가장 높다. 따라서 고위 전망에서 생산 측면의 수익률이 낮기는 하지만, 보유가치 측면의 수익률이 한층 더 높기 때문에 고위 전망의 자본투자 수익률이 가장 높은 것으로 볼 수 있다.
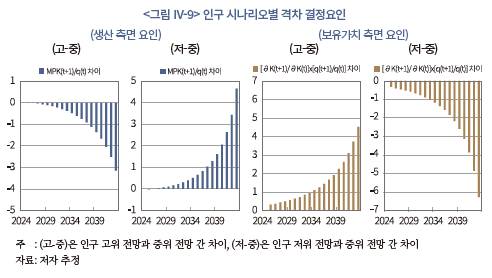
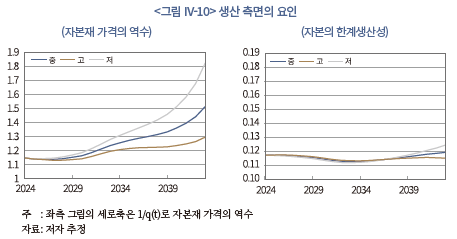
상기 분석 결과 중 저위 전망에서 생산 측면의 수익률이 전반적으로 높은 것은 자본재 가격이 상대적으로 크게 하락한 데 따른 것으로 분석된다. <그림 IV-10>은 생산 측면의 요인을 자본재 가격의 역수(1/q(t))와 자본의 한계생산성으로 세분화하여 나타내고 있는데, 저위 전망에서 자본재 가격의 하락(좌측)이 매우 가파르다는31) 점을 알 수 있다. 아울러 시간이 경과함에 따라 자본의 한계생산성도 저위 시나리오에서 더 높아지면서 생산 측면의 수익률이 상대적으로 커지는 요인으로 작용한다.32) 다만, 이러한 경향은 2030년대 후반에 들어서야 관측되고, 자본재 가격 요인에 비해 시나리오 간 격차도 크지 않기 때문에 자본의 한계생산성이 그 차이를 주도한다고 보기는 어렵다.
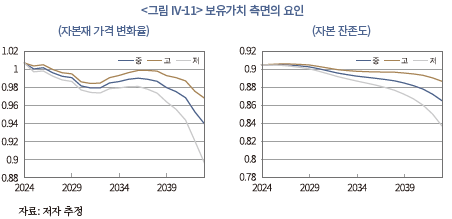
한편, 고위 전망에서 보유가치 측면의 수익률이 더 높게 나타난 것은 자본재 가격 변화율과 자본 잔존도가 모두 영향을 미친 것으로 판단된다. 이는 <그림 IV-11>을 통해 확인할 수 있다. 고위 전망은 자본재 가격 변화율(좌측)에서 차이를 보이기도 하지만, 자본 잔존도에서도 지속적으로 격차를 나타낸다. 따라서 두 요인에서 모두 양(+)의 격차가 존재하면서 여타 시나리오보다 고위 시나리오의 자본투자 수익률이 높아지게 된다. 이는 고위 시나리오에서 자본재 수요(투자)가 상대적으로 높게 유지되는 데 따른 결과로 해석할 수 있다.33)
나. 고연령층의 노동시장 참여
앞 절에서는 25~49세 인구에 대한 중위 전망을 기본으로 하여 해당 인구가 상위 또는 하위 전망에 따라 변화하는 경우와 비교해 보았다. 여기에서는 고연령층의 노동시장 참여가 증가하는 경우를 가정하여 자본투자 수익률을 전망해 보고자 한다. 인구 구조상 50세 이상 고연령층의 비중이 커지고, 보건의료 수준도 개선되어 경제활동 참가 기간이 길어질 수 있으므로 이러한 시나리오에 대한 분석도 상당한 의미가 있을 것으로 생각된다.
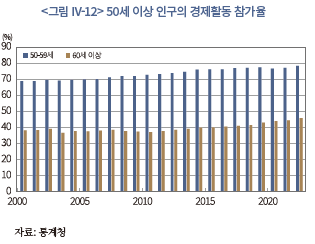
<그림 IV-12>는 2000년 이후 국내 50세 이상 인구의 경제활동 참가율을 50~59세와 60세 이상으로 구분하여 나타내고 있다. 기간에 따라 다소 부침이 존재하기는 하지만, 전반적으로는 두 연령대 모두 경제활동 참가율이 점진적으로 증가하는 추세를 보인다. 50~59세 인구의 경제활동 참가율은 2000년 68.8%에서 2022년 78.4%로 10%p 가까이 증가하였고, 60세 이상은 2000년의 38.2%에서 2022년의 45.8%로 약 8%p 증가하였다. 따라서 두 연령대 간 경제활동 참여도에는 다소 큰 차이가 있지만, 증가폭 측면에서는 큰 격차가 없다는 점을 알 수 있다.
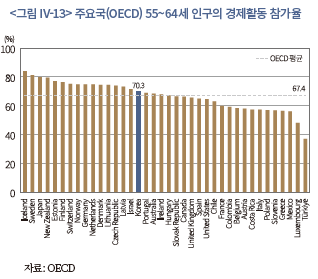
이러한 추세는 앞으로도 지속될 가능성이 있다. 보건의료 수준 개선과 함께, 최근의 청년층 교육 수준 향상34)도 향후 고연령층의 경제활동 참가율을 높이는 요인으로 작용할 수 있기 때문이다. 즉, 고연령 인구의 인적자본이 고도화되면서 동 연령층이 생산활동에서 유효하게 활용될 수 있는 여지가 과거에 비해 커질 수 있다. 아울러 우리나라보다 고연령층의 경제활동 참가율이 높은 선진국이 다수 존재한다는 점도 참고할 만한 사실이라 생각된다. 이는 <그림 IV-13>에 제시된 OECD 국가 내 55~64세 인구의 경제활동 참가율(2022년)을 통해 확인할 수 있다. 우리나라의 경우 해당 연령대의 경제활동 참가율은 70.3%로 OECD 평균보다 높지만, 독일(75.3%), 일본(80.1%), 스웨덴(81.7%) 등에 비해서는 낮고 그 격차도 다소 큰 편이다. 이러한 점을 볼 때 고연령층의 노동시장 참여 증가는 어느 정도 실현 가능성이 존재하는 시나리오라고 판단된다.
본 시나리오의 구체적인 가정은 다음과 같다. 먼저, 노동시장 참여는 통상적인 노동 투입이 이루어지는 상황을 상정하였다. 이는 신규 참가자의 노동시간과 질이 전체 근로자 평균과 다르지 않은 경우를 의미한다. 다음으로, 노동시장에 추가로 참여하는 연령은 50~64세로 한정하였다. 현실적으로 65세 이상보다는 해당 연령대의 추가 참가 가능성이 더 높은 것으로 판단되기 때문에 50세 이상 전체를 대상으로 고려하지는 않았다. 마지막으로, 해당 연령대의 노동 공급은 20년간 총 7%p 증가(매년 +0.35%p)하는 것으로 가정하였다. 이는 OECD 내 상위 10% 수준(경제활동 참가율)과의 차이35)를 반영하여 해당 격차만큼 노동 공급이 증가하는 상황을 전제한 것이다. 이러한 시나리오 하에서 2043년의 노동투입량은 중위 인구 전망(기본 시나리오)보다 약 5.5% 증가하는 것으로 계산된다. 그리고 이 비율은 고위 인구 전망(2043년)의 경우보다 약 0.8%p 높은 수준이다.
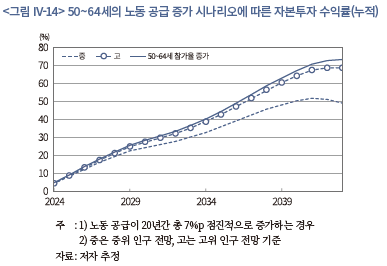
<그림 IV-14>는 상기 시나리오에 따라 산출한 자본투자 수익률(누적)을 나타내고 있다. 그림에는 중위 및 고위 인구 전망의 자본투자 수익률도 표시되어 있는데, 본 시나리오의 결과는 가장 상단에 있는 실선에 해당한다. 이 결과에 따르면 향후 20년간 누적수익률은 약 73%로 연평균으로는 약 2.8%로 환산된다. 이는 앞서 분석한 중위 인구전망의 누적수익률보다 24%p 높은 수준으로, 고연령층의 노동시장 참가가 자본투자 수익률에 상당한 영향을 미칠 수 있음을 시사한다. 즉, 향후 50~64세 인구의 노동시장 참가가 점차 증가한다면, 인구 감소의 부정적 영향을 부분적으로 상쇄하여 자본투자 수익률을 높이는 효과가 있다는 점이다. 특히, 본 시나리오와 같은 수준으로 노동 공급이 증가할 경우, 고위 인구 전망에서보다 근소하게(4%p) 높은 자본투자 수익률을 얻을 수 있다는 결과에 주목할 필요가 있다.
다. 여성의 노동시장 참여
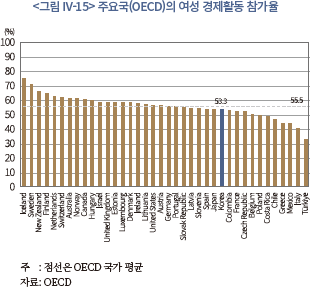
본 절에서는 또 다른 가능성으로 여성의 노동시장 참여가 증가하는 경우를 고려해 보고자 한다. 잘 알려진 바와 같이, 우리나라 여성의 경제활동 참가율은 남성보다 상당히 낮은 수준이며36) 주요국에 비해서도 낮은 편이다. <그림 IV-15>는 OECD 국가들의 여성 경제활동 참가율(2021년)을 표시하고 있는데, 우리나라 여성의 참가율은 53.3%로 나타난다. 이는 OECD 평균인 55.5%을 하회하는 수준으로 OECD 내 백분위로는 하위 32%에 속한다. 그리고 상위 5개 국가37)의 평균(67.9%)과 비교하면 약 15%p의 큰 격차를 보인다.
여성의 경제활동 참가가 저조하다는 것은 우리나라의 노동 및 인적 자본 활용에 상당한 제약이 존재한다는 점을 의미한다. 하지만 한편으로는, 관련 제도와 여건 개선 등을 통해 노동시장 참여를 유도함으로써 성장잠재력을 제고할 수 있는 여지가 존재하는 것으로도 볼 수 있다. 이러한 시각을 바탕으로, 여성의 노동 공급이 20년간 총 10%p(매년 0.5%p) 증가하여 통상적인 노동 투입으로 이어지는 시나리오에 대해 분석해 보고자 한다. 동 증가폭은 고연령층에 대한 시나리오 분석과 마찬가지로 OECD 내 상위 10% 국가와의 격차를 반영한 수준이다.
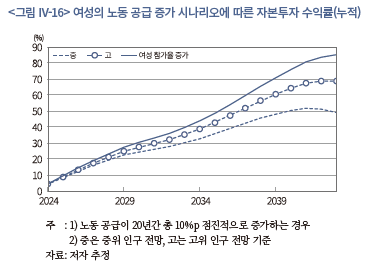
<그림 IV-16>은 상기 시나리오에 따라 산출된 자본투자 수익률(누적)을 나타내고 있다. 향후 20년간 누적수익률은 약 85%로 연평균으로는 약 3.1%에 해당한다. 이는 앞서 중위와 고위 인구 전망에 따른 결과보다 각각 36%p 및 16%p 높은 수준으로 상당히 큰 증가폭을 보인다. 동 시나리오에 의하면, 20년 후 노동투입량은 인구 중위 전망 대비 7.9% 증가하게 되는데, 이는 고연령층의 참여가 증가하는 경우(중위 전망 대비 +5.5%)보다 큰 수준이다. 이에 따라 고연령층의 참여 증가 시나리오에서보다 본 시나리오에서 자본투자 수익률이 더 높게 산출되는 것으로 볼 수 있다.
라. 총요소생산성 변화
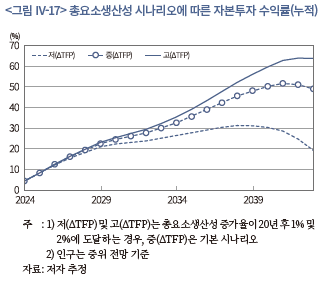
마지막으로 총요소생산성에 대한 시나리오로부터 산출된 결과에 대해 논의하고자 한다. III장에서 살펴본 바와 같이 우리나라의 총요소생산성 증가율(연평균)은 1980~1990년대에는 3.8%, 2000년 이후에는 2.4%로 낮아졌고, 최근에는 대체로 2% 내외의 수준을 보이고 있다. 기본 시나리오에서는 2010년 이후의 자료를 반영하여 매년 1.7% 증가하는 것으로 설정하였는데, 본 시나리오 분석에서는 20년간 점진적으로 1%까지 하락하거나 2%까지 상승하는 경우를 추가로 고려하였다. 여기에서 하방 시나리오(1%)는 우리나라의 기술 진보율의 전반적인 위상이 OECD 상위권에서 중위권으로 낮아지는 경우로 생각해 볼 수 있다.38) 그리고 상방 시나리오(2%)는 최근 3년간(2019~2021년)의 국내 총요소생산성 증가율 평균(1.9%)에 가까운 수준으로 수렴하는 경우에 해당한다.
<그림 IV-17>은 20년 후 총요소생산성 증가율이 2%(고) 및 1%(저)인 경우의 누적 자본투자 수익률을 보이고 있다. 이 결과에 따르면, 향후 20년간 누적수익률은 각각 64%(고) 및 20%(저)로 기본 시나리오와 대비할 때 각각15%p 및 29%p의 차이를 보인다. 이러한 격차는 향후 자본투자 수익률 흐름에 있어 인구뿐만 아니라 기술 발전의 영향도 결코 간과할 수 없다는 점을 보여준다.
시나리오 분석에서 총요소생산성은 독립적인 요인으로서, 이것이 특정 집단이나 전체 인구의 노동시장 참여에 영향을 주지 않는 것을 전제하고 있다. 하지만 총요소생산성 증가의 원천인 기술 진보는 계층별 경제활동 참가율에도 영향을 미칠 수 있다. 긍정적인 측면에서 보면, 기술 발전이 전반적인 생산성뿐만 아니라 노동력 자체에도 보완적39)으로 작용하여 작업 수행에 따르는 유·무형의 제약을 완화할 수 있다. 따라서 이러한 방향의 기술 발전은 여성과 고연령층의 노동시장 참가를 확대하는 데에도 기여할 수 있다. 그리고 그 결과, 위의 시나리오 분석 결과보다 높은 수준의 자본투자 수익률이 실현될 가능성도 있을 것으로 생각된다.
Ⅴ. 요약 및 결론
본 연구에서는 이론적인 모형을 바탕으로 자본투자 수익률을 추정하고, 주식 수익률과의 관계에 대해 살펴보았다. 실증 분석 결과에 따르면, 자본투자 수익률은 주식 수익률의 장기 추이를 설명하는 데 유용하게 활용될 수 있음을 알 수 있었다. 이는 주가가 기업의 투자와 생산 등 실물 경제활동과 무관하지 않으며, 주식 수익률의 움직임을 설명하는 데 있어 이러한 배경에 대한 고찰이 필요하다는 점을 의미한다.
지난 40년여 간의 자료를 분석한 결과, 2000년 이후 자본투자 수익률은 이전에 비해 평균적으로 하락한 것으로 나타났다. 이는 고도 성장기가 저물고 저성장 국면으로 진입한 데 따른 결과로 생각될 수도 있다. 하지만, 자본투자 수익률의 구성 요소에 대해 세부적으로 살펴보면서 보다 흥미로운 결과를 발견할 수 있었다. 기간별로 비교해 볼 때, 2000년대 들어 보유가치 측면의 수익률은 전반적으로 하락하였지만, 생산 측면의 수익률은 소폭 상승했다는 점이 특징적으로 나타났다. 그리고 이 중 생산 측면의 수익률이 상승한 것은 자본재 가격의 하락이 미친 영향이 컸기 때문으로 분석되었다. 세부적으로 보면, 자본의 한계생산성은 지속적으로 하락하는 추세를 나타내면서 생산 측면의 수익률을 낮추는 요인으로 작용하였다. 반면, 자본재 가격은 1990년경부터 하락세가 두드러지면서 수익률을 높이는 요인으로 작용하여 상반된 양상을 보였다. 이러한 결과는, 추가 자본투입을 통한 생산량 증가폭은 감소하였지만, 자본재를 보다 저렴하게 구입할 수 있게 됨으로써 생산 측면의 수익률이 향상되었다는 점을 의미한다.
본 연구에서는 이러한 실증 분석과 함께, 여러 시나리오를 통해 향후 20년간의 자본투자 수익률을 전망해 보았다. 통계청의 중위 인구 전망을 이용한 시나리오 분석 결과에 따르면, 인구 증가율과 자본투자 수익률의 시계열이 상당히 유사한 방향성을 가지고 움직이는 특징을 보였다. 아울러 인구 수준별 시나리오에 따르면, 20년 후 고위와 저위 인구 시나리오에 따른 누적수익률은 중위 대비 ±20%p에 가까운 격차를 나타냈다. 이상의 결과들은 인구 변화가 구조적인 요인으로 작용하면서 그 전개 방향에 따라 자본투자 수익률이 크게 변화할 수 있다는 점을 시사한다.
위의 시나리오 분석은 인구를 제외한 연령별·성별 경제활동 참가 정도는 현재와 동일할 것이라는 가정을 바탕으로 한다. 하지만, 현실적으로는 인구 고령화, 인적 자본의 고도화, 노동시장 참여 여건 개선 등이 진행되면서 다른 전제가 필요할 수도 있다. 이러한 점을 고려하여 고연령층과 여성의 노동 공급이 확대되는 경우를 각각 가정한 시나리오에 대해 추가로 분석해 보았다. 결과에 따르면, 50~64세 인구와 여성의 노동 공급이 일정하게 증가하여 각각 7%p 및 10%p 확대되는 경우, 자본투자 수익률(누적)은 기본 시나리오 대비 24%p와 36%p 상승하는 것으로 전망되었다.
실물 경제뿐만 아니라 주식 시장의 성장을 위해서도 기술 진보와 생산성 향상의 중요성은 분명히 강조되어야 한다. 하지만 향후 당면하게 될 경제환경을 그려보면, 이러한 자명한 결론보다는 노동시장 참여 여건을 개선하여 기술 진보를 보완할 수 있는 가능성에 대해 주목할 필요가 있다. 특히, 앞서 고연령층 및 여성의 노동 공급 증가를 가정한 시나리오에서의 수익률은 20년 후 총요소생산성 증가율이 2% 수준까지 상승하는 경우보다 높은 것으로 나타났다. 2000년 이후 총요소생산성 증가율이 1980~1990년대의 절반 수준으로 낮아졌다는 점을 고려할 때, 총요소생산성 증가율 추세의 상승 전환은 쉽지 않은 과제이다. 이러한 의미에서 위의 결과는 노동시장에 대한 개선을 병행함으로써 기술 발전 둔화를 보완해 나가야 함을 시사한다.
고연령층과 여성의 노동시장 참여는 가용 노동자원을 확대할 수 있는 주요 원천이지만, 이를 단기간에 크게 끌어올리는 데에는 한계가 있을 수 있다. 하지만, 본 연구의 시나리오 분석은 점진적인 개선도 중요한 동력으로 작용하면서 자본투자 수익률을 크게 제고할 수 있다는 점을 함축한다. 아울러 고연령층과 여성의 경제활동이 활성화된 주요국의 사례에 비추어 볼 때, 효율적인 정책 개발과 실행이 뒷받침된다면 긍정적인 시나리오가 현실화될 수 있을 것이다.
1) 일반균형 모형에서 확률적 할인인자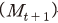 는 가계의 선호에 의해 그 형태가 결정되는데, IV장에서 구체적으로 제시하도록 하겠다.
는 가계의 선호에 의해 그 형태가 결정되는데, IV장에서 구체적으로 제시하도록 하겠다.
2) 일차적인 의미는 투자에 사용된 최종재 1단위(분자, 1)를 최종재 1단위 투자로 추가된 자본량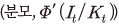 으로 나눈 것이다. 여기에서
으로 나눈 것이다. 여기에서 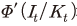 가 작을수록 동일한 양의 자본을 추가하기 위한 대가로 더 많은 최종재가 소요되므로 자본재의 상대가격이 높아지는 것으로 풀이할 수 있다. 그리고 이는 라그랑지 승수가 그림자 가격(shadow price)이라는 일반적인 해석과도 일치한다.
가 작을수록 동일한 양의 자본을 추가하기 위한 대가로 더 많은 최종재가 소요되므로 자본재의 상대가격이 높아지는 것으로 풀이할 수 있다. 그리고 이는 라그랑지 승수가 그림자 가격(shadow price)이라는 일반적인 해석과도 일치한다.
3) 엄밀하게는 보유한 자본에서 얻게 될 미래의 배당 가치를 평가한 것이다.
4) Restroy and Rockinger(1994)의 첫 번째 명제(proposition 1)에서 생산함수와 자본조정비용이 선형동차 함수(linearly homogeneous function)이면 두 수익률 간에 동일성이 성립한다는 결과로, 모형의 콥-더글라스 생산함수와 식 (3)의 자본조정비용은 해당 조건을 만족한다. 참고를 위해 <부록>에 도출 과정을 수록하였다.
5) 자본 대 투자 비율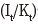 이 일정한 수준에 수렴하여 자본조정비용이 발생하지 않는 장기균형상태(steady-state)를 상정하면
이 일정한 수준에 수렴하여 자본조정비용이 발생하지 않는 장기균형상태(steady-state)를 상정하면 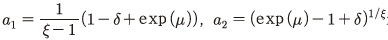 가 성립한다(Jermann, 1998). 여기에서
가 성립한다(Jermann, 1998). 여기에서 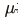 는 성장률로 2010~2021년 중 평균을 적용하였다.
는 성장률로 2010~2021년 중 평균을 적용하였다.
6) 생산함수의 모수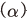 는 0.31, 감가상각률
는 0.31, 감가상각률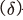 은 8%로 설정된다.
은 8%로 설정된다. 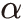 는 2010년 이후 민간 부문의 부가가치 대비 영업잉여 비율의 평균,
는 2010년 이후 민간 부문의 부가가치 대비 영업잉여 비율의 평균, 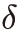 는 시산 결과(6%: 조태형 등(2012))와 기존 문헌(10%: 배병호 등(2018))의 평균을 적용하였다.
는 시산 결과(6%: 조태형 등(2012))와 기존 문헌(10%: 배병호 등(2018))의 평균을 적용하였다.
7) 아울러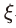 가 무한대에 가까워지면 자본재와 최종재의 가격이 같아지지만,
가 무한대에 가까워지면 자본재와 최종재의 가격이 같아지지만, 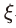 이 유한한 양수이면 자본재와 최종재의 가격이 달라지게 된다.
이 유한한 양수이면 자본재와 최종재의 가격이 달라지게 된다.
8) GMM에서는 도구 변수(instrumental variable)로 과거 3년간 민간 소비 증가율의 평균을 사용하였다.
9) 지수 편제와 관련된 자세한 내용은 한국은행(2009)을 참조하기 바란다.
10) 주거용 건물은 민간의 주거 서비스를 위해 소비되므로 기업의 생산에 활용되는 자본재로 보기는 어렵다. Farhi and Guorio(2018)도 본고와 동일한 방식으로 민간 투자를 측정하였다.
11) <부록>에는 보다 구체적인 내용과 함께 산출된 거시지표의 기술 통계량, 총요소생산성 계산 방식, 성장회계에 따른 요인별 기여도 등이 수록되어 있다.
12) 귀무가설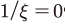 이 통계적으로 기각됨을 확인하였다.
이 통계적으로 기각됨을 확인하였다.
13) 추정에서 KOSPI의 지수수익률 대신 배당의 재투자가 반영된 총수익률(total return)을 사용하는 경우에도 실증 분석 결과에는 큰 차이가 없는 것으로 나타났다. <부록>에 총수익률을 이용한 추정 결과가 제시되어 있다.
14) 식 (6)은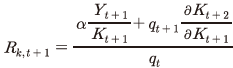 이며
이며 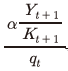 은 생산 측면,
은 생산 측면, 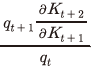 는 보유가치 측면의 수익률에 해당한다.
는 보유가치 측면의 수익률에 해당한다.
15) 보다 엄밀하게는 외환위기 발생(1997년) 전후를 기준으로 평균이 유의하게 하락한 것으로 나타난다.
16) <그림 III-5>의 자본재 가격은 모형과 동일한 개념에 따라 자본재의 가격을 최종재(민간 소비)의 가격으로 나눈 상대가격이다. 자본재의 가격은 생산용 민간 자본투자(주거용 건물 및 재고 제외)에 속하는 각 항목의 GDP 디플레이터와 물량 지표를 이용하여 연쇄 라스파이레스 방식으로 산출한 것이다.
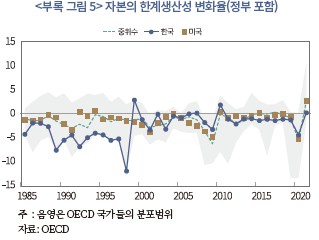
17) OECD 국가들의 경우 민간 부문만을 대상으로 한 자본생산성 변화율 자료 확보가 어려워 정부 부문까지 포함된 자료를 사용하였다. 하지만, 동일한 기준(정부 부문 포함)으로 산출된 자료로 비교하더라도 이러한 평가는 달라지지 않는다. 해당 결과는 <부록 3>에 제시되어 있다.
18) OECD 국가들의 자료에는 <그림 III-7>과 유사하게 정부 부문까지 포함되어 있지만, 동일한 기준(정부 부문까지 포함)으로 산출된 자료로 비교하더라도 이러한 평가는 달라지지 않는다. 해당 결과에 대해서는 <부록 3>에 제시되어 있다.
19) <그림 III-11>에 별도로 추세선을 표시하지는 않았지만, OECD 국가들의 중위수와 평균은 모두 유의하게 하락하는 모습을 나타낸다.
20) 엄밀하게는 한계 증가분이라는 표현이 맞지만, 자본은 감가상각과 자본조정비용에 의해 감소하게 되므로 직관적인 의미에 보다 가까운 잔존도라는 표현을 사용하였다.
21) 자본조정비용이 존재하지 않는 경우에는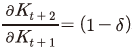 가 된다.
가 된다.
22)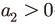 이므로 이러한 관계가 항상 성립된다.
이므로 이러한 관계가 항상 성립된다.
23) 2000년 전후 평균 측면에서 보면 자본재 가격 변화율도 일부 영향을 미쳤지만, 자본 잔존도가 추세적으로 하락한 영향이 주도하였으므로 여기에 초점을 맞추었다.
24) t+1부터 t+5시점까지의 I/K 비율 평균을 종속변수, t-4부터 t시점까지의 TFP 증가율 평균을 독립변수로 한 예측식(predictability regression)에서 TFP 증가율은 I/K 비율을 유의하게 예측하며 설명력(R2=0.66)도 매우 높은 것으로 나타났다.
25) 균형 경로에서 소비와 GDP는 동일한 변화율을 따르는 것으로 가정한다.
26)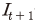 에 대한 선택 구간은 10만개로 분할한 그리드가 사용되는데 선택 구간은
에 대한 선택 구간은 10만개로 분할한 그리드가 사용되는데 선택 구간은 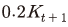 이하의 양수로 설정하였다. 이 방식을 통해 최소화된 목적함수 값(Euler equation error)은 10-9를 넘지 않으며 대부분 10-10 미만이다.
이하의 양수로 설정하였다. 이 방식을 통해 최소화된 목적함수 값(Euler equation error)은 10-9를 넘지 않으며 대부분 10-10 미만이다.
27) 2024년 이후 기간의 전망을 위해서는 2023년의 투자가 필요한데, 이 값은 2024년의 민간 총생산(GDP) 증가율에 대한 자체 전망치(2%)를 적용하여 산출하였다. 즉, 동 성장률에 상응하는 2024년의 자본량을 도출하면 2023년의 투자가 계산된다.
28) 노동투입량 추세의 경우, 비선형(3차식) 추세의 설명력(R2=0.94)이 선형 추세(R2=0.69)보다 훨씬 높아 비선형식을 이용하였다. 아울러 2차식을 이용할 경우에도 정점 도달 시기에는 큰 차이가 없다.
29) 소비자물가상승률로 실질화된 통안증권(1년) 수익률의 평균을 사용하였다.
30) 식 (4)에 일반화 적률법을 적용하여 추정한 결과를 활용하였다. 추정치의 95% 신뢰구간은 (0.61, 3.60)인데, 시나리오 분석에서 사용된 값은 점 추정치(2.1)에 가까운 수치이다. 박명호·오종현(2015)에서도 본고와 동일한 위험회피도가 사용되었다.
31) 저위 전망에서는 필요 자본 규모가 더 작기 때문에 자본재의 가치가 상대적으로 낮게 평가되는 것으로 해석할 수 있다.
32) 이는 투자 규모가 크게 축소된 영향이 누적되어 중위나 고위 시나리오에 비해 자본축적도가 상대적으로 낮아진 데 기인한 것으로 볼 수 있다.
33) 즉, 고위 전망에서는 자본재 수요(투자)가 상대적으로 높기 때문에 가격 하락폭이 비교적 완만한 모습을 보이고, 자본의 잔존도도 높게 유지된다는 점이다.
34) 우리나라 25~34세 인구의 고등(대학)교육 이수율은 2000년 38.5%에서 2021년 69.3%로 대폭 증가하였다. 2021년 기준 동 연령대의 고등교육 이수율은 OECD 중 1위이며 OECD 평균(47.1%)을 20%p 이상 상회한다.
35) OECD 통계에서는 55~64세 기준 자료만 가용하기 때문에 이 연령대의 격차를 기준으로 하였다.
36) 2022년 기준 남성과 여성의 경제활동 참가율은 각각 73.5% 및 54.6%로 20%p에 가까운 격차가 존재한다.
37) 상위 5개국은 아이슬란드(75.1%), 스웨덴(70.9%), 뉴질랜드(66.1%), 핀란드(64.6%), 네덜란드(62.8%)이다.
38) 앞 장에서 언급한 바와 같이 OECD의 총요소생산성 증가율에는 정부 부문이 포함되어 있어 정확한 직접 비교가 어렵다는 문제가 있다. 다만, 미국의 민간 부문(business sector) 총요소생산성 증가율과 연계해서 생각할 때 위와 같은 추론이 가능하다. 미국의 1980~2021년 중 민간 부문 총요소생산성 증가율의 평균은 약 0.9%로 전제치의 하한인 1%에 가까운데, OECD 그룹 내에서 미국의 총요소생산성 증가율(정부 포함)은 중위 수준에 해당한다. 단, 이는 과거 자료를 기준으로 순위를 비교한 것으로, 1%로 낮아지는 것이 향후 미국의 총요소생산성 변화율에 수치상 근접하게 될 것이라는 의미가 아님을 밝혀 둔다. 여기에서 미국 민간 부문의 수치는 샌프란시스코 연준(https://www.frbsf.org/economic-research/indicators-data/)에서 제공되는 자료(Solow의 잔차, 계열명은 ‘dtfp’)이다.
39) 물리력을 보조하는 로봇 등이 일반화되는 경우를 생각할 수 있다.
40) Restroy & Rockinger(1994)의 보조 정리 1(Lemma 1)을 참조할 수 있다.
41) 통계청의 민간 부문 종사자수와 평균 근로시간을 곱한 수치이다.
42) 해당 기업 목록과 자료 분석에 관련된 조언을 주신 자본시장연구원 김준석 박사께 감사드린다.
참고문헌
박명호·오종현, 2015, 『조세재정정책의 거시경제적 효과 분석을 위한 DSGE 모형 구축: GIMF 모형의 이해와 활용』.
배병호·유진혁·지정구, 2018, 경제전망 및 정책분석을 위한 BOKDSGE 모형 개선 결과, 『조사통계월보』 2018년 1월호.
조태형·이병탁·도경탁, 2012, 자산별 내용연수의 추정에 관한 연구, 『국민계정리뷰』 2012년 1호.
한국거래소, 2018, 『신규 총수익지수 7종 발표』.
한국은행, 2009, 『연쇄가중 경제성장률 이해』.
한국은행, 2020, 『한국의 국민대차대조표 해설』.
Boldrin, M., Christiano, L.J., Fisher, J.D.M, 2001, Habit persistence, asset returns, and the business cycle. American Economic Review 91, 149–66.
Christiano, L.J., Fitzgerald T.J., 2003, The band pass filter, International Economic Review 44(2), 435-465.
Cochrane, J.H, 1991, Production-based asset pricing and the link between stock returns and economic fluctuations, Journal of Finance 46(1), 209-237.
Croce, M.M., 2014, Long-run productivity risk: A new hope for production-based asset pricing? Journal of Monetary Economics 66, 13-31.
Farhi, E., Guorio, F., 2018, Accounting for macro-finance trends: Market power, intangibles, and risk premia, Brookings Papers on Economic Activity, Fall 2018.
Hansen, L.P., Singleton, K.J., 1983, Stochastic consumption, risk aversion, and the temporal behavior of asset returns, Journal of Political Economy 91(2), 249-265.
Hayashi, F., 1982, Tobin's marginal q and average q: A neoclassical interpretation, Econometrica 50(1), 213-224.
International Monetary Fund, 2019, The price of capital goods: A driver of investment under threat? World Economic Outlook, April 2019.
Jermann, U., 1998, Asset pricing in production economics, Journal of Monetary Economics 41, 257–75.
Kaltenbrunner, G., Lochstoer, L.A., 2010, Long-run risk through consumption smoothing, Review of Financial Studies 23(8), 3190-3224.
Organisation for Economic Co-operation and Development, 2001, Measurement of aggregate and industry-level productivity growth, Measuring Productivity-OECD Manual.
Restoy, F., Rockinger, M., 1994, On stock market returns and returns on investment, Journal of Finance 49, 543–56.
<부록>
1. 주식 수익률과 자본투자 수익률의 이론적 관계
기업 가치를 배당과 계속 가치의 항으로 나타내면, 가치 함수는 다음과 같이 표현할 수 있다.
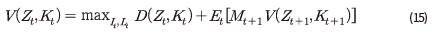
위 식에서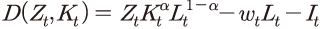 이며 계속 가치는 배당 후 주가에 해당하므로
이며 계속 가치는 배당 후 주가에 해당하므로 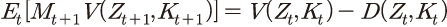 로 나타낼 수 있다. 따라서 주식 수익률
로 나타낼 수 있다. 따라서 주식 수익률 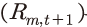 은 다음과 같이 표현된다.
은 다음과 같이 표현된다.
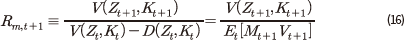
한편, 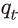 를 자본축적식에 대한 라그랑지 승수로 두면 일계 조건에 따라 다음과 같은 식이 도출된다.
를 자본축적식에 대한 라그랑지 승수로 두면 일계 조건에 따라 다음과 같은 식이 도출된다.
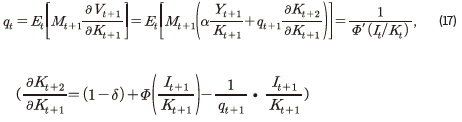
식 (17)의 양변을 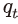 로 나누면, 다음의 식을 얻을 수 있다.
로 나누면, 다음의 식을 얻을 수 있다.
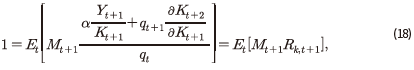
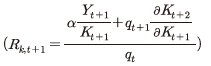
여기에서 기업 가치 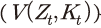 는 자본
는 자본 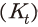 에 선형성40을 가지므로 다음이 성립한다.
에 선형성40을 가지므로 다음이 성립한다.
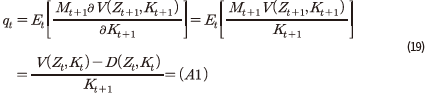
그리고 아래의 식이 성립한다.
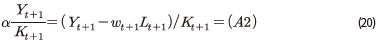
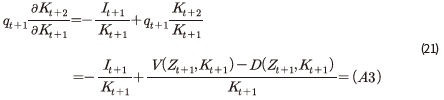
위에서 도출된 항 (A1)~(A3)을 이용하여 자본투자 수익률을 표현하면, 다음과 같이 자본투자 수익률과 주식 수익률의 동일성이 성립함을 알 수 있다.
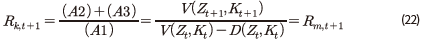
2. 거시 데이터 및 기술 통계량
먼저, 민간 총생산을 산출하는 데에는 한국은행의 경제통계 시스템(ECOS)에 수록된 「2.1.2.1.3. 경제활동별 GDP 및 GNI(명목)」 및 「2.1.2.1.4. 경제활동별 GDP 및 GNI(실질)」자료를 이용한다. 여기에서는 기본적으로 정부 부문을 제외한 세부문의 생산액을 대상으로 한다. 각 세부문의 명목 생산액을 실질 생산액으로 나누어 가격 디플레이터를 구하고, 연쇄 라스파이레스 방식을 통해 합산함으로써 민간 부문의 실질 GDP를 계산한다.
투자는 ECOS의 「2.1.6.2.1. 주체별 총자본형성(명목)」에 제공되는 민간 부문의 총자본형성(명목)에서 주거용 투자를 차감한 값을 연쇄 라스파이레스 가격 지수로 실질화하여 산출한다. 여기에는 비주거용 건물, 토목건설, 운송장비, 기계류, 연구개발, 기타 지식재산생산물이 포함된다. 가격 디플레이터는「2.1.6.1.3. 자본재형태별 총자본형성(명목)」 및 「2.1.6.1.4. 자본재형태별 총자본형성(실질)」에서 주거용 건물 및 재고를 제외한 투자 항목의 명목 및 실질 금액을 이용하여 산출하게 된다.
자본 스톡은 ECOS에서 국민대차대조표 자료인 「2.4.5.1. 제도부문별 생산자본스톡
(명목)」 및 「2.4.5.2. 제도부문별 생산자본스톡(실질)」중 민간 부문의 자본 스톡 자료를 이용하였다. 투자와 마찬가지로 주거용 건물을 제외한 고정자산의 명목 및 실질 금액을 이용하여 가격 디플레이터를 구하고, 연쇄 라스파이레스 방식으로 비주거용 자본 스톡의 실질액을 산출한다.
전술한 연쇄 라스파이레스 방식에 따른 t기의 실질(물량,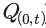 ) 및 가격 지수
) 및 가격 지수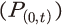 는 연환지수(link factor)인
는 연환지수(link factor)인 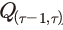 ,
, 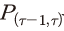 를 각각 이용하여 식 (23) 및 (24)와 같이 계산된다.
를 각각 이용하여 식 (23) 및 (24)와 같이 계산된다.
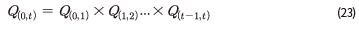
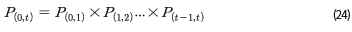 여기에서 연환지수는
여기에서 연환지수는 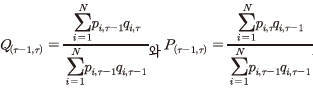 로 정의되며 하첨자
로 정의되며 하첨자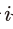 는 세부문,
는 세부문, 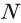 는 세부문의 수를 의미한다.
는 세부문의 수를 의미한다.
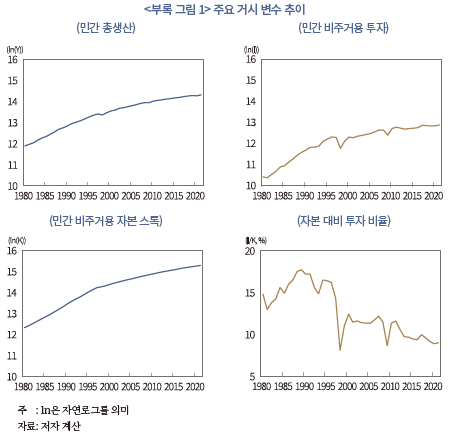
아래의 <부록 그림 1>에는 이상의 방법으로 산출한 민간 부문의 총생산, 비주거용 투자 및 자본 스톡의 실질액(로그)과 자본 대비 투자 비율(I/K)이 나타나 있다. 아울러 <부록 표 1>에는 민간 총생산, 투자, 자본의 증가율과 자본 대비 투자 비율에 대한 주요 기술 통계량이 제시되어 있다.
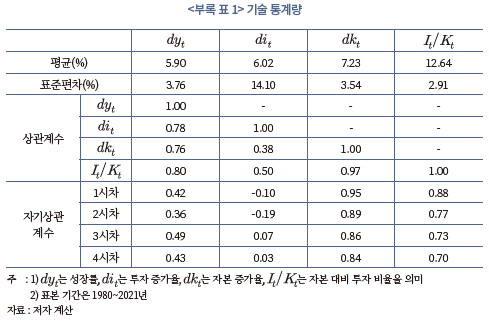
3. 총요소생산성 변화 및 성장 기여도
총요소생산성의 변화는 식 (1)에 제시된 콥-더글라스 생산함수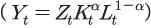 를 이용하여 Solow의 잔차로 측정한다. 이는 앞서 구축한 민간 부문의 총생산
를 이용하여 Solow의 잔차로 측정한다. 이는 앞서 구축한 민간 부문의 총생산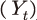 , 자본
, 자본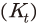 및 노동 투입41)
및 노동 투입41)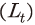 자료를 이용하여 산출된다. 생산함수에서
자료를 이용하여 산출된다. 생산함수에서 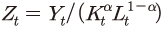 로 주어지므로 총요소생산성의 변화는 다음과 같이 계산된다.
로 주어지므로 총요소생산성의 변화는 다음과 같이 계산된다.
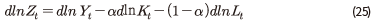
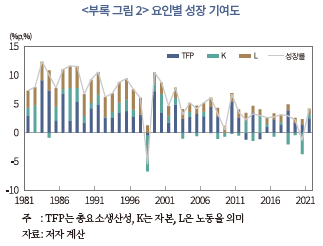
한편, 이와 같은 방법으로 총요소생산성의 변화를 구하면, 각 요인들의 성장률에 대한 기여도를 분석할 수 있다. 그 결과는 <부록 그림 2>에 제시되어 있다. 여기에서 알 수 있듯이 2000년대 들어 성장률이 전반적으로 낮아진 가운데, 각 요인의 성장 기여도도 모두 평균적으로 축소되었다. 2000년 전후로 요인별 기여도의 평균을 보면, 총요소생산성은 3.8%p에서 이후 2.4%p 낮아졌고 자본은 3.3%p에서 1.4%p로 크게 축소되는 한편, 2000년대 들어 음(-)의 기여도를 보이는 경우가 빈번해졌다. 노동의 기여도는 2000년대 이전 1.2%p에서 이후 영에 가까운 수준(0.1%p)으로 낮아져 정체된 모습을 나타내고 있다.
4. 총수익률(total return)을 이용한 추정 결과
총수익률 지수의 공식 통계(한국거래소 발표)는 2011년부터 존재한다. 이전 기간에 대해서는 상장회사협의회의 자료(TS2000)를 이용하여 KOSPI 지수 내 기업별 배당을 집계하여 연장한 자료를 사용하였다. 단, TS2000에는 상장폐지 기업들의 상장폐지 이후 기간의 자료, 신규 상장 기업들의 상장 이전 기간의 자료, 기업인수목적회사(SPAC) 및 외국 기업들의 자료 등이 포함되어 있어 이들은 집계에서 제외하였다.42
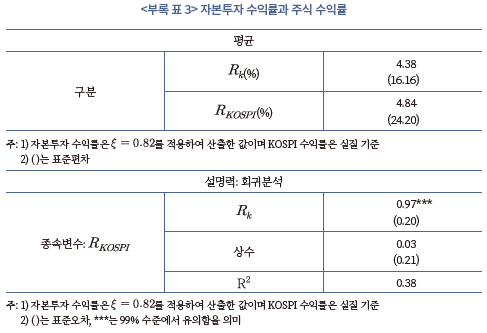
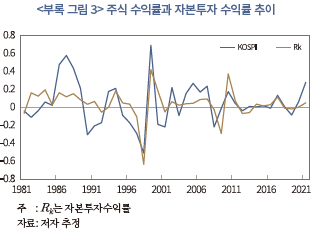
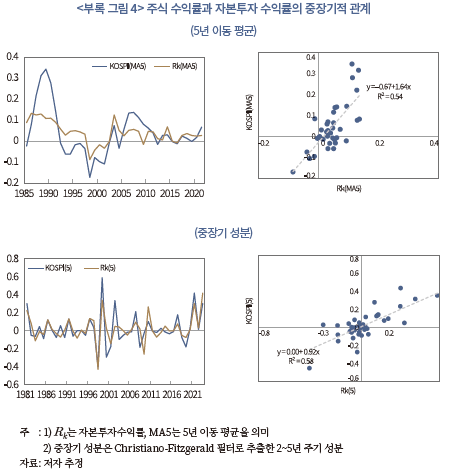
아래의 <부록 표 2>와 <부록 표 3>은 총수익률을 이용하여 본문과 동일한 방법으로 추정한 자본조정비용의 모수 및 자본투자 수익률과 주식 수익률간 관계를 보여주고 있다. 아울러 <부록 그림 3>과 <부록 그림 4>는 자본투자 수익률과 주식 수익률의 연간 자료, 두 수익률의 5년 이동 평균과 중장기 성분(Christiano-Fitzgerald 필터 이용)의 추이를 나타내고 있다.

5. 정부 부문이 포함된 자료를 이용한 국제 비교
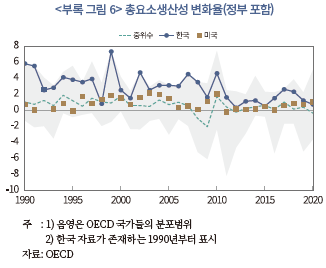
아래 <부록 그림 5>와 <부록 그림 6>은 OECD 국가들을 대상으로 정부 부문이 포함된 자본의 한계생산성 변화율과 총요소생산성 변화율을 각각 나타내고 있다.
거시적인 관점에서 주식 수익률은 실물 부문, 특히 기업의 자본투자 수익률(capital investment return)과 밀접하게 연관되어 있다. 기업의 자본은 투자를 통해 축적된 생산요소로서 수익을 지속적으로 창출하는 자산이다. 기업을 생산요소의 집합체로 단순화하여 생각한다면, 기업의 가치는 자본의 가치에 직결되면서 주식 수익률은 자본투자 수익률에 따라 움직이는 것으로 볼 수 있다. 본 연구는 이러한 관점에서 1980년 이후 우리나라의 주식 수익률을 자본투자 수익률을 통해 분석하고 20년 시계의 장기 전망을 제시한다.
1980년대 이후 국내외 경제환경에는 많은 변화가 있었다. 국내적으로 1990년대 중반까지의 고도 성장기에는 기업들의 사업 범위가 크게 확장되면서 인적·물적 자본도 빠르게 축적되었다. 하지만 그 과정에서 기업 부문의 부실과 비효율이 누적되었고, 외환위기를 계기로 대규모 구조조정이 뒤따랐다. 대외적으로는 1990년대 들어 각국의 세계화와 경제 개방이 본격적으로 진행되면서 글로벌 분업과 경쟁이 본격화되었다. 그 결과 거래비용이 감소하고 원자재나 자본재 등 생산요소에 대한 접근성도 한층 높아졌다. 이러한 변화가 미친 영향은 실물 경제활동과 직접적으로 연결된 자본투자 수익률에도 반영되어 있을 것으로 생각된다.
한편, 앞으로의 흐름을 내다볼 때, 다가올 국내 경제환경 변화 중 가장 중요한 것으로 인구 감소와 고령화를 들 수 있다. 2021년에 발표된 통계청의 인구 전망(중위)에 따르면, 경제활동이 가장 활발한 연령대인 25~49세의 인구는 2024년 이후 20년간 약 24% 감소할 것으로 예상된다. 또한 65세 이상 인구의 비중은 2024년 19.4%에서 2043년 36.1%로 2배 가까이 증가할 것으로 전망된다. 장비 및 자동화 등을 통한 대체가 어려울 경우, 핵심 경제활동 인구의 감소는 생산 설비 운영이나 서비스 공급 인력의 부족으로 이어지고 자본투자 수익률에도 영향을 미칠 수 있다. 따라서 본 연구는 인구 전망을 바탕으로 향후 국내 자본투자 수익률에 대해 전망하고 시나리오별로 비교·분석하고자 한다. 여기에서는 중위 인구 전망을 기본 시나리오로 하되, 인구 전반, 고연령 계층 및 여성의 노동시장 참여, 총요소생산성 증가율에 대한 시나리오도 함께 고려하여 그 결과를 분석하였다.
이론적인 측면에서 본 연구는 Cochrane(1991)과 Restroy & Rockinger(1994)의 연구를 배경으로 한다. Cochrane(1991)은 자본투자 수익률을 이론적으로 도출하고, 자본투자 수익률이 주식 수익률과 높은 양(+)의 상관관계를 보인다는 실증 분석 결과를 제시한 바 있다. 그리고 Restroy & Rockinger(1994)는 일정한 가정 하에서 주식 수익률과 자본투자 수익률이 이론적으로 동일하다는 점을 보였다. 본 연구의 분석은 이들 연구에서 밝혀진 주식 수익률과 자본투자 수익률 간의 연관성에 기초하고 있다. 아울러 본 연구는 모형 등 기본적인 접근 방법에서 Jermann(1998), Kaltenbrunner & Lochstoer(2010), Croce(2014) 등과도 유사한 측면이 있다. 하지만, 상기 연구들은 추정보다는 이론적 기제와 수치적 실험을 통해 주식 프리미엄 퍼즐을 해결하는 데 초점을 맞추고 있어 목적상 차이가 있다. 한편, 미국을 대상으로 한 Farhi & Gourio(2018)는 연구 목적에 있어 본 연구와 어느 정도 공통점을 가진다. 해당 연구는 1980년대 중반 이후 자본수익률과 무위험이자율의 장기적 추이에 관심을 가지고 생산요소와 시장지배력 등의 구조적 측면을 통해 분석하였다. 다만 본 연구와는 달리, Farhi & Gourio(2018)에서는 주식 수익률과의 연관성에 대한 평가 없이 자본투자 수익률만 독립적으로 분석되었고 장기 전망도 포함되지 않았다.
우리나라의 경우, 주식 수익률에 대해 위와 같은 접근 방식으로 장기적인 시각에서 분석한 연구는 부족한 실정이다. 이러한 측면에서 본 연구는 국내 주식 수익률과 자본투자 수익률 간의 관계, 그리고 자본투자 수익률의 동인이 된 경제환경을 조망하기 위한 참고 자료가 될 수 있을 것으로 생각된다. 본 연구가 제시하는 주요 결과 중 하나로, 자본투자 수익률이 중장기 주식 수익률에 대해 실증적으로 높은 설명력을 가진다는 점을 들 수 있다. 이는 특수한 가정 없이 표준적인 거시 모형을 통해 도출되었기 때문에 국내 자산 가격(asset pricing) 연구에 의미 있게 기여할 수 있을 것으로 생각된다. 아울러 자본투자 수익률에 대한 장기 전망은 노동시장과 관련된 정책적 시사점과 함께, 모형의 폭넓은 활용 가능성을 보여준다는 점에서도 의의를 가진다고 생각된다.
본고의 구성은 다음과 같다. 먼저, Ⅱ장에서는 자본투자 수익률에 대한 이론적인 배경을 제시하고 구성 요소들의 경제적 의미에 대해 설명한다. Ⅲ장에서는 실증 분석을 통해 1980년 이후 우리나라의 자본투자 수익률을 추정하고, 주식 수익률과의 관계 등 주요 특징에 대해 논의하도록 하겠다. 그리고 Ⅳ장에서는 경제환경 변화에 대한 여러 시나리오를 바탕으로 향후 국내 자본투자 수익률에 대해 전망하고 결과를 비교한다. 마지막으로 Ⅴ장에서는 분석 결과와 시사점에 대해 종합적으로 논의하면서 보고서를 맺도록 하겠다.
II. 이론적 배경
자본투자 수익률은 보편적인 거시 모형을 바탕으로 하여 도출된다. 모형에는 무한 계획기간(infinite time horizon) 하에서 최종재를 생산하는 대표 기업이 존재한다. 그리고 이 경제에서는 총요소생산성
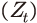 이 외생적으로 주어지고 기업의 투자에 자본조정비용이 수반되는 것으로 가정한다. 이러한 환경 하에서 기업은 매 t기마다 가치(
이 외생적으로 주어지고 기업의 투자에 자본조정비용이 수반되는 것으로 가정한다. 이러한 환경 하에서 기업은 매 t기마다 가치(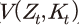 , value function)를 극대화하는 생산요소 투입량을 아래와 같이 결정하게 된다.
, value function)를 극대화하는 생산요소 투입량을 아래와 같이 결정하게 된다.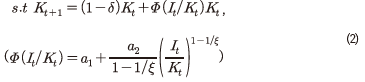
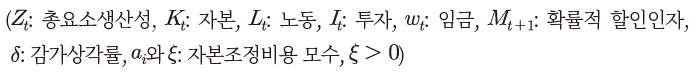
식 (1)은 기업의 목적함수로 우변에 있는
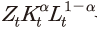 는 기업의 생산함수
는 기업의 생산함수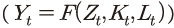 에 해당한다. 이는 통상적인 가정에 따라 규모에 대한 수확불변(constant returns to scale)인 콥-더글라스 생산함수로 설정되었다. 식 (1) 우변의 두 번째
에 해당한다. 이는 통상적인 가정에 따라 규모에 대한 수확불변(constant returns to scale)인 콥-더글라스 생산함수로 설정되었다. 식 (1) 우변의 두 번째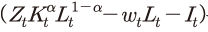 은 배당
은 배당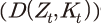 에 해당한다. 그리고 마지막 항인
에 해당한다. 그리고 마지막 항인 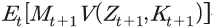 는 일반적으로 계속 가치(continuation value)로 정의된다. 기업은 무한 계획기간 하에서 다음 기에도 동일한 형태의 최적화 문제를 풀게 되므로 이 항이 가산되고 목적함수는 축차적인(recursive) 형태를 띠게 된다. 여기에서 미래의 총요소생산성은 확률적으로 주어지기 때문에 계속 가치는 기댓값으로 결정되게 된다.
는 일반적으로 계속 가치(continuation value)로 정의된다. 기업은 무한 계획기간 하에서 다음 기에도 동일한 형태의 최적화 문제를 풀게 되므로 이 항이 가산되고 목적함수는 축차적인(recursive) 형태를 띠게 된다. 여기에서 미래의 총요소생산성은 확률적으로 주어지기 때문에 계속 가치는 기댓값으로 결정되게 된다.목적함수 아래에 있는 식 (2)는 제약조건으로 자본축적식을 나타내고 있다. 앞서 언급한 바와 같이 본 모형에서는 실물 부문의 마찰 요인으로 투자에 대한 자본조정비용이 존재하는데, 그 함수적인 형태는 Jermann(1998), Boldrin et al.(2001), Kaltenbrunner & Lochstoer(2010), Croce(2014) 등과 동일하게 설정된다. 자본조정비용의 구체적인 형태는 식 (2)를 변형하여 정리한 식 (3)에서
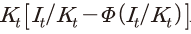 로 표현된 항이다. 자본조정비용이 존재하지 않는 경우의 자본축적식은
로 표현된 항이다. 자본조정비용이 존재하지 않는 경우의 자본축적식은 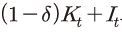 로 감가상각 후 잔존 자본에 신규 투자가 추가되는 형태가 된다.
로 감가상각 후 잔존 자본에 신규 투자가 추가되는 형태가 된다.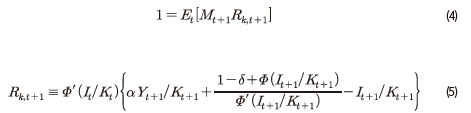
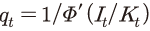 가 도출되는데 이는 최종재에 대한 자본재의 상대가격이 된다.2) 그리고 식 (5)를
가 도출되는데 이는 최종재에 대한 자본재의 상대가격이 된다.2) 그리고 식 (5)를 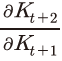 이용하여 정리하면, 자본투자 수익률은 식 (6)과 같이 표현될 수 있다.
이용하여 정리하면, 자본투자 수익률은 식 (6)과 같이 표현될 수 있다.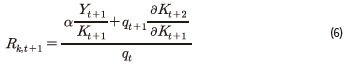
 은 자본의 한계생산성, 즉, 자본투입 증가를 통해 추가로 산출되는 한계생산물(marginal product)에 해당한다. 따라서 자본의 한계생산성을 t기 자본재의 가격(분모,
은 자본의 한계생산성, 즉, 자본투입 증가를 통해 추가로 산출되는 한계생산물(marginal product)에 해당한다. 따라서 자본의 한계생산성을 t기 자본재의 가격(분모, 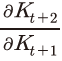 는 t+1기에 자본이 축적됨에 따라 t+2기에 추가적으로 자본이 증가하는 부분을 나타낸다. 이는 t+1기에 축적된 자본이 그 다음기에 잔존하는 양을 의미하는 것으로도 해석할 수 있다. 이러한 잔존 자본에 t+1기의 자본재 가격을 곱한 값
는 t+1기에 자본이 축적됨에 따라 t+2기에 추가적으로 자본이 증가하는 부분을 나타낸다. 이는 t+1기에 축적된 자본이 그 다음기에 잔존하는 양을 의미하는 것으로도 해석할 수 있다. 이러한 잔존 자본에 t+1기의 자본재 가격을 곱한 값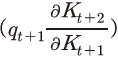 은 잔존 자본의 가치이며, 이를 t기 자본재의 가격(분모, )으로 나누면 자본을 보유함으로써 t+1기에 얻게 될 수익률로 볼 수 있다. 따라서 이상을 요약하면, 첫 번째 항(분모 포함)은 생산 측면의 수익률, 두 번째 항(분모 포함)은 보유가치3) 측면의 수익률로 경제적인 의미를 부여할 수 있다.
은 잔존 자본의 가치이며, 이를 t기 자본재의 가격(분모, )으로 나누면 자본을 보유함으로써 t+1기에 얻게 될 수익률로 볼 수 있다. 따라서 이상을 요약하면, 첫 번째 항(분모 포함)은 생산 측면의 수익률, 두 번째 항(분모 포함)은 보유가치3) 측면의 수익률로 경제적인 의미를 부여할 수 있다.한편, 식 (1)에서 기업가치
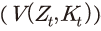 는 배당이 포함된 주가와 동일하며, 계속 가치
는 배당이 포함된 주가와 동일하며, 계속 가치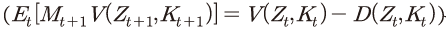 는 배당 후 주가에 해당한다. 이에 따라 t+1기의 배당 전 주가를 분자, t기의 배당 후 주가를 분모로 하여 t+1기의 주식 수익률
는 배당 후 주가에 해당한다. 이에 따라 t+1기의 배당 전 주가를 분자, t기의 배당 후 주가를 분모로 하여 t+1기의 주식 수익률다만, 동 모형은 현실성의 측면에 있어서는 한계점이 존재한다. 2000년대 들어 국내 기업의 해외 생산기지가 상당히 확대되었기 때문에 이를 고려하여 실증 분석 모형을 구축하는 것이 이상적인 접근일 것이다. 하지만, 자료의 제약 등으로 인해 폐쇄 경제(closed economy)를 가정하여 모형을 구축했다는 점을 밝혀 둔다.

본 장에서는 실증 분석 방법론에 관해 설명하고 자본투자 수익률의 추정 결과와 주요 특징에 대해 논의한다. 여기에서 실증 분석은 크게 두 부분으로 구성된다. 첫 번째는 자본투자 수익률 모형의 모수 추정 결과와 주식 수익률에 대한 자본투자 수익률의 설명력에 대한 평가이다. 이 부분에서는 이론적으로 구축된 모형이 주식 수익률의 장기 시계열을 설명하는 데 유용하게 활용될 수 있는지 확인해 보고자 한다. 두 번째는 자본투자 수익률의 구성 요소에 내재된 주요 특징에 대한 분석이다. 여기에서는 자본투자 수익률을 요인별로 분해하고, 각 요인의 시계열적 특징을 실물 경제 부문의 변화와 연관지어 고찰해 보고자 한다.
1. 방법론
실증 분석에서는 기본적으로 모형의 모수 추정과 해당 추정치를 이용한 자본투자 수익률의 산출이 필요하다. 추정 모형은 식 (5)와 자본투자 수익률과 주식 수익률 간 동일성을 이용하여 식 (8)과 같은 형태로 도출된다.

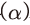 와 감가상각률
와 감가상각률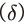 의 경우, 데이터 및 기존 문헌 등을 바탕으로 결정된다.6) 한편, 모형 내 각 변수의 시계열은 국민계정 자료와 주가 지수 등을 이용하여 구축되는데 관련 내용은 다음 절에서 별도로 설명하도록 하겠다.
의 경우, 데이터 및 기존 문헌 등을 바탕으로 결정된다.6) 한편, 모형 내 각 변수의 시계열은 국민계정 자료와 주가 지수 등을 이용하여 구축되는데 관련 내용은 다음 절에서 별도로 설명하도록 하겠다.전술한 모수 중에서
비선형성을 갖는 식 (8)은 별도의 변형 없이 최소자승법(Least Squares: LS) 및 일반화 적률법(Generalized Method of Moments: GMM)8)을 각각 적용하여 추정된다. 동 추정에서는 국소해(local optimum)나 불안정성 등의 문제를 피하기 위해 강건한 방식인 그리드 탐색법(grid search)을 적용하였다. 그리고 추정치의 표준오차는 500개의 표본을 이용한 부트스트랩(bootstrap) 방법에 따라 산출된다.
2. 데이터
실증 분석 모형(식 (8))을 추정하기 위해서는 주식 수익률과 식 (8)의 우변에 포함된 각 실물 경제 지표의 시계열 자료가 필요하다. 자료 구축에서 한 가지 유념했던 점은 식 (8)의 좌변에 있는 주식 수익률은 기본적으로 민간 부문만을 포괄하는 지표라는 것이다. 이 경우, 자본투자 수익률(우변)을 구성하는 실물지표에 정부 부문이 포함될 경우 일관성이 부족해지는 문제가 있을 수 있다. 따라서 우변에 속하는 실물지표는 모두 민간 부분을 대상으로 하여 자료를 구축하였다.
아울러, 민간 부문에 대한 집계 자료는 세부문의 가격 디플레이터와 물량지표(실질액)를 이용하여 합산(aggregation)했다는 점을 밝혀 둔다. 우리나라의 국민총생산 자료는 연쇄 라스파이레스(chained Laspeyres) 방식9)에 의해 작성되는데, 이 방식의 특성상 세분류 항목의 실질액을 단순 합산한 결과가 대분류의 실질액과 일치하지 않게 된다. 이러한 비가법성(non-additivity)을 고려하여 국민계정 편제시와 동일한 방법을 적용하여 민간 부문의 실질액을 구하였다. 세부적으로는, 민간 총생산의 경우 경제활동별 GDP에서 비정부 부문의 실질 생산액을 GDP 편제 방식에 따라 산출하여 사용하였다. 그리고 투자는 민간 부문의 투자 항목 중 주거용 건물 및 재고를 제외한 생산용 자본투자를 대상으로 하였다.10) 여기에는 비주거용 건물, 토목건설, 운송장비, 기계류, 연구개발, 기타 지식재산생산물이 포함된다. 자본 스톡은 공식 통계인 국민대차대조표 자료를 이용하였는데, 투자와 마찬가지로 생산용 자본(민간 부문)을 대상으로 하였다.11) 자본투자 수익률은 실질 개념이므로 주식 수익률은 KOSPI 지수를 소비자물가로 실질화한 자료를 사용하였다.
실증 분석의 대상 기간은 1980년부터 2021년까지이며 연간 자료를 바탕으로 추정된다. 자본 스톡의 공식 통계인 국민대차대조표가 연간 단위로 작성되기 때문에 자료의 주기는 이를 기준으로 하였다. 본 연구는 주식 및 자본투자 수익률의 중장기적인 흐름에 초점을 두고 있으므로, 저빈도의 자료를 사용하더라도 분석의 목적에서 크게 벗어나지 않을 것으로 판단된다.
3. 실증 분석 결과
여기에서는 전술한 방법론과 데이터를 통해 산출된 실증 분석 결과를 제시한다. 본 절의 전반부에서는 추정된 모수와 자본투자 수익률에 대해 살펴보고, 자본투자 수익률이 주식 수익률을 의미 있게 설명할 수 있음을 확인하도록 한다. 후반부에서는 자본투자 수익률 결정요인의 시계열적인 특징에 대하여 구조적 요인들의 변화와 연관지어 논의하고자 한다.
가. 모수 및 자본투자 수익률
<표 III-1>에는 최소자승법(LS)과 일반화 적률법(GMM)으로 추정한 자본조정비용의 모수(


<그림 III-1>은 추정된 자본투자 수익률과 주식 수익률의 움직임을 명시적으로 나타내고 있다. 앞서 제시된 통계량이 의미하듯이, 자본투자 수익률은 주식 수익률에 비해 한층 완만하게 움직이지만, 두 수익률은 전반적으로 유사한 방향성을 가지고 있음을 확인할 수 있다. 이상의 결과는 단기적인 측면에서 주식 수익률이 기업의 실물 투자 활동과 그 성과에 어느 정도 연동되어 있다는 점을 시사한다.


그리고 이동 평균을 이용한 회귀식의 결정계수
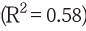 . 이러한 결과는 중장기적인 주가의 흐름을 이해하는 데 있어 자본투자 수익률이 유용하게 활용될 수 있음을 의미한다고 하겠다.
. 이러한 결과는 중장기적인 주가의 흐름을 이해하는 데 있어 자본투자 수익률이 유용하게 활용될 수 있음을 의미한다고 하겠다.나. 주요 특징: 개관
앞 절의 결과에서 주식 수익률의 중장기적인 움직임을 설명하는 데 자본투자 수익률이 높은 설명력을 가진다는 점을 알 수 있었다. 본 절에서는 자본투자 수익률을 구성하는 각 요인들에 대해 보다 자세히 살펴보면서 주요 특징에 대해 논의하고자 한다. 여기에서는 먼저 전반적인 특징에 대해 개관하고, 세부적인 내용에 대해서는 다음 절에서 다루도록 하겠다.
II장에서 언급했듯이 자본투자 수익률
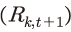 은 식 (6)과 같이 생산 측면과 보유가치 측면의 수익률로 나누어 볼 수 있다.14) <표 III-3>은 이러한 구분에 따라 2000년 전후 기간의 자본투자 수익률 평균과 그 차이를 생산과 보유가치 측면의 수익률로 나누어 제시하고 있다. 우선 (A)와 (B)열을 보면, 2000년 이후 자본투자 수익률은 3.58%로 이전(5.49%)에 비해 평균적으로 약 2%p 하락15)했다는 점이 나타난다. 이는 일차적으로, 1980~1990년대의 고도 성장기를 지나 저성장 국면으로 진입한 데 따른 결과로 풀이할 수도 있다. 하지만 식 (6)에 따라 각 구성 요소를 분해하면 다른 관점에서 자본투자 수익률의 변화에 대해 분석해 볼 수 있다.
은 식 (6)과 같이 생산 측면과 보유가치 측면의 수익률로 나누어 볼 수 있다.14) <표 III-3>은 이러한 구분에 따라 2000년 전후 기간의 자본투자 수익률 평균과 그 차이를 생산과 보유가치 측면의 수익률로 나누어 제시하고 있다. 우선 (A)와 (B)열을 보면, 2000년 이후 자본투자 수익률은 3.58%로 이전(5.49%)에 비해 평균적으로 약 2%p 하락15)했다는 점이 나타난다. 이는 일차적으로, 1980~1990년대의 고도 성장기를 지나 저성장 국면으로 진입한 데 따른 결과로 풀이할 수도 있다. 하지만 식 (6)에 따라 각 구성 요소를 분해하면 다른 관점에서 자본투자 수익률의 변화에 대해 분석해 볼 수 있다.
다. 주요 특징: 생산 측면의 수익률
Ⅱ장에서 논의한 바와 같이 생산 측면의 수익률은 자본의 한계생산성
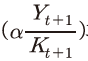 과 자본재의 가격
과 자본재의 가격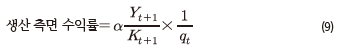





앞서 언급했듯이 2000년 이후 총요소생산성이 자본의 한계생산성 변화에 미친 양(+)의 기여도는 이전 기간에 비해 줄어든 경향이 있다. <그림 III-10>에 제시된 장기 시계열을 보면, 총요소생산성 증가율은 대체로 둔화되는 모습을 보이는 가운데 최근에는 2% 내외의 수준을 나타내고 있다. 총요소생산성 증가율은 기술 진보 정도를 포착하는 주요 지표이므로 이와 같은 흐름은 성장잠재력이 축소되고 있음을 의미할 수 있다. 다소 우려되는 상황이라는 점은 분명하지만, 총요소생산성 증가율의 둔화는 비단 우리나라뿐만 아니라 주요국들도 경험하고 있는 현상으로 생각된다. <그림 III-11>은 1985년 이후 OECD 국가들의 총요소생산성 증가율18)을 표시하고 있는데, 이 국가들도 전반적으로 둔화되는 모습19)을 보이면서 우리나라와 유사한 양상을 나타낸다.

라. 주요 특징: 보유가치 측면의 수익률
보유가치 측면의 수익률은 식 (10)과 같이 자본재의 가격변화율인
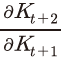 를 곱한 것으로, 다음 기에도 남게 될 자본을 t+1기의 시장가격으로 판매하는 경우를 가정한 수익률로 생각할 수 있다.
를 곱한 것으로, 다음 기에도 남게 될 자본을 t+1기의 시장가격으로 판매하는 경우를 가정한 수익률로 생각할 수 있다.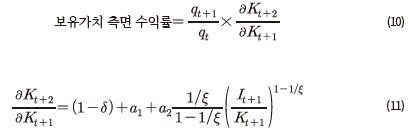
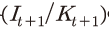 에 의해 결정됨을 의미한다. 만약 자본조정비용이 존재하지 않는다면 식 (11)이 상수21)로 단순화된다. 하지만, 그렇지 않은 경우에는
에 의해 결정됨을 의미한다. 만약 자본조정비용이 존재하지 않는다면 식 (11)이 상수21)로 단순화된다. 하지만, 그렇지 않은 경우에는 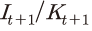 비율이 높을수록 잔존 자본이 커지게 되는데22), 이는 두 가지 의로 해석될 수 있다. 먼저, 신규투자가 기존에 축적된 자본과 같은 비율로 증가해야 잔존 자본이 동일하게 유지된다는 점을 의미한다. 다른 한편으로는, t+1기에 동일한 크기의 투자
비율이 높을수록 잔존 자본이 커지게 되는데22), 이는 두 가지 의로 해석될 수 있다. 먼저, 신규투자가 기존에 축적된 자본과 같은 비율로 증가해야 잔존 자본이 동일하게 유지된다는 점을 의미한다. 다른 한편으로는, t+1기에 동일한 크기의 투자 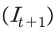 를 할지라도 기존에 설치된 자본 규모
를 할지라도 기존에 설치된 자본 규모 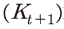 가 크다면, t+2기에 추가로 축적되는 자본이 축소되는 것으로 해석될 수도 있다. 즉, 자본축적 이후에 후속 투자가 충분하게 이루어지지 않으면 유효 자본의 증가에 제약이 따르는 것을 의미한다고 하겠다.
가 크다면, t+2기에 추가로 축적되는 자본이 축소되는 것으로 해석될 수도 있다. 즉, 자본축적 이후에 후속 투자가 충분하게 이루어지지 않으면 유효 자본의 증가에 제약이 따르는 것을 의미한다고 하겠다.
앞서 식 (11)을 바탕으로 논의한 바와 같이, 모형에 따르면 투자가 자본과 동일한 변화율로 증가해야 자본 잔존도가 일정하게 유지된다. 이를 바탕으로 생각할 때, 국내 자본 잔존도가 감소한 것은 지속적인 투자를 통해 이를 유지하는 데 한계가 따랐기 때문으로 판단된다. 1990년대 중반까지는 대기업을 중심으로 투자가 빠르게 확대되었지만, 외환위기 이후의 대규모 구조조정, 성장잠재력 하락 등으로 인해 기업들이 이전처럼 적극적으로 투자를 확대하기가 어려워졌을 것이다. 또한, <표 Ⅲ-4>와 <그림 III-9>에서 살펴본 것처럼 노동 공급의 정체로 인한 영향도 있을 것으로 판단된다. 즉, 자본의 한계생산성은 추가적인 노동 투입을 통해 개선될 수 있지만, 이를 확대할 수 있는 여력이 축소되면서 투자를 제약한 측면도 간과할 수 없을 것으로 생각된다.
여기에서 성장잠재력 측면에서의 제약은 <그림 III-14>에 나타난 총요소생산성(TFP) 증가율과 자본 대비 투자 비율(I/K)의 관계를 통해 추론해 볼 수 있다. 그림에 표시된 TFP 증가율은 과거 t-4부터 t시점까지 5년간의 TFP 증가율 평균, I/K 비율은 미래 t+1부터 t+5시점까지 5년간의 I/K 비율 평균이다. 여기에서 두 계열은 밀접한 양의 상관관계를 가지면서 과거의 TFP 증가율이 미래의 I/K 비율을 유의하게 예측하는 것으로 분석된다.24) 이러한 점으로 볼 때, 투자가 둔화되면서 자본 잔존도가 하락한 데에는 TFP 증가율 둔화로 성장잠재력이 축소된 것이 일정 부분 영향을 미쳤을 것으로 생각된다.

III장에서는 자본투자 수익률이 주식 수익률의 중장기적인 흐름을 상당 부분 설명할 수 있다는 점을 실증적으로 확인할 수 있었다. 또한, 분석 결과에 따르면 자본투자 수익률은 보유가치 측면의 수익률 하락이 큰 영향을 미치면서 2000년대 들어 평균적으로 하락한 것으로 나타났다. 그리고 이러한 보유가치 측면의 수익률 하락에는 총요소생산성 증가율 하락과 노동 공급 정체 등이 투자를 제약함으로써 자본 잔존도가 낮아진 것이 원인으로 작용했다고 판단된다.
향후에도 자본투자 수익률은 기술 진보나 노동자원의 가용도에 따라 크게 달라질 수 있다. 따라서 본 장에서는 이러한 경제환경 변화에 대한 시나리오를 바탕으로 국내 자본투자 수익률을 전망하고 그 결과에 대해 논의하고자 한다. 특히, 인구 감소와 고령화는 현재 예상되는 가장 중요한 환경 변화로 노동부존량에 직접적인 영향을 미치는 만큼, 이와 관련된 시나리오에 초점을 맞추고자 한다. 여기에서는 방법론에 대해 먼저 간략히 설명한 다음, 시나리오 분석 결과를 제시하도록 하겠다.
1. 방법론
시나리오 분석은 외생변수인 노동부존량과 총요소생산성의 전제치를 바탕으로 내생변수들의 균형값을 산출하는 방식을 이용한다. 기업의 투자와 자본투자 수익률
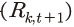 은 상기 외생변수의 움직임에 따라 결정되는 내생변수에 해당한다. 여기에서
은 상기 외생변수의 움직임에 따라 결정되는 내생변수에 해당한다. 여기에서 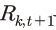 은 III장에서 설명한 대로 식 (12)와 같이 표현될 수 있다.
은 III장에서 설명한 대로 식 (12)와 같이 표현될 수 있다.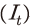 와 자본량
와 자본량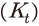 이 주어진다면, 자본축적식에 의해 t+1기의 자본량
이 주어진다면, 자본축적식에 의해 t+1기의 자본량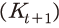 이 결정될 수 있다. 또한 외생적으로 주어진 노동부존량
이 결정될 수 있다. 또한 외생적으로 주어진 노동부존량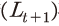 과 총요소생산성
과 총요소생산성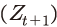 을 이용하면 t+1기의 생산량
을 이용하면 t+1기의 생산량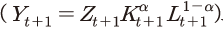 도 계산될 수 있다. 그러면 식 (12)에서 t+1기의 투자
도 계산될 수 있다. 그러면 식 (12)에서 t+1기의 투자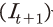 를 제외한 여타 변수는 모두 그 값이 결정되는데, 이때
를 제외한 여타 변수는 모두 그 값이 결정되는데, 이때 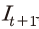 은 최적화 조건인 투자에 대한 오일러 방정식을 이용하여 산출될 수 있다.25)
은 최적화 조건인 투자에 대한 오일러 방정식을 이용하여 산출될 수 있다.25)
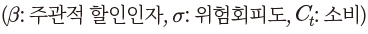
비확률적 균형에서 오일러 방정식은 식 (13)과 같이 정리되는데, 최적 투자는 이 방정식이 성립하는
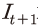 가 된다. 수치적으로는 식 (14)와 같이 정의된 목적함수를 최소화하는 값에 해당하며 그 해는 그리드 탐색을 통해 산출된다.26)
가 된다. 수치적으로는 식 (14)와 같이 정의된 목적함수를 최소화하는 값에 해당하며 그 해는 그리드 탐색을 통해 산출된다.26)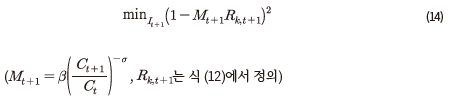
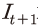 이 주어지면, t+2기의 자본량이 결정되게 된다. 그러면 위와 같은 일련의 연산 과정을 동일하게 반복하여 나머지 변수들의 t+2기 값을 산출할 수 있다. 이러한 과정을 순차적으로 적용하여 20년간의 시계열을 생성하면 주어진 시나리오에 대한 전망이 완료된다.27)
이 주어지면, t+2기의 자본량이 결정되게 된다. 그러면 위와 같은 일련의 연산 과정을 동일하게 반복하여 나머지 변수들의 t+2기 값을 산출할 수 있다. 이러한 과정을 순차적으로 적용하여 20년간의 시계열을 생성하면 주어진 시나리오에 대한 전망이 완료된다.27)각 변수의 전망치를 산출하기 위한 실제 연산에서는 모형 내 모수값들과 함께 노동부존량과 총요소생산성에 대한 전제치가 필요하다. 노동부존량

2. 시나리오 분석 결과
시나리오 분석에서는 통계청의 중위 인구 전망을 기본 시나리오로 하여 향후 20년간의 자본투자 수익률을 전망한다. 다만, 인구·노동정책, 기술 발전의 전개 양상 등에 따라 경제환경이 유동적으로 변화할 수 있기 때문에 기본 시나리오는 상당히 제한된 측면만을 조명한 것일 수 있다. 이러한 점을 고려하여 인구 전반, 고연령 인구의 노동시장 참여, 여성의 노동시장 참여, 총요소생산성 증가율에 대한 시나리오를 추가로 적용하여 전망치를 산출하고 결과를 비교하도록 하겠다. 이를 통해 여러 환경 변화가 자본투자 수익률에 미치는 영향에 대해 보다 종합적인 시각에서 평가해 볼 수 있을 것으로 생각된다.
가. 인구 시나리오
통계청의 장래 인구추계에서는 가정에 따라 저위, 중위, 고위 경로의 인구가 전망되어 있다. 전망 경로별로 수준의 차이는 있지만, 저출산의 장기화로 인해 우리나라의 인구가 당분간 감소할 것으로 예측된다는 점은 공통적이다. <그림 IV-3>은 세 종류의 전망치를 나타내고 있는데, 좌측 그림에서 실선은 중위 전망에 따른 25~49세 인구, 위와 아래의 점선은 각각 고위 및 저위 전망에 따른 동 연령의 인구에 해당한다. 이 중 중위 전망에 따르면, 2043년의 25~49세 인구는 약 1,370만명으로 2024년 대비 24% 감소하게 된다. 그리고 고위와 저위 전망에 따른 2043년의 인구는 중위 전망과 약 ±70만명의 차이를 보인다(<그림 IV-3> 우측). 전체 시계열을 보면 고위 및 저위 전망은 대체로 중위 전망을 중심으로 하여 대칭적인 모습을 보인다.




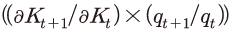 측면으로 나누어 표시하고 있다. 제시된 결과에 따르면, 자본투자 수익률은 2000년 이후와 유사한 특징을 가지고 변화할 것으로 예상된다. 실증 분석 결과를 보면, 2000~2021년 중에는 생산 측면의 양(+)의 영향보다는 보유가치 측면의 음(-)의 영향이 더 크게 작용한 것으로 추정되었다. <그림 IV-7>은 전망에서도 생산 측면의 수익률은 대체로 자본투자 수익률을 높이는 방향으로 작용하지만, 보유가치 측면의 수익률은 이를 낮추는 방향으로 작용함을 나타낸다. 그리고 결과적으로는 보유가치 측면의 하방 영향이 전반적으로 크게 작용하면서 자본투자 수익률이 낮아지는 모습을 보인다. 이러한 점을 볼 때, 향후에도 실증 분석에서 나타났던 경향이 당분간 지속될 것으로 예상할 수 있다.
측면으로 나누어 표시하고 있다. 제시된 결과에 따르면, 자본투자 수익률은 2000년 이후와 유사한 특징을 가지고 변화할 것으로 예상된다. 실증 분석 결과를 보면, 2000~2021년 중에는 생산 측면의 양(+)의 영향보다는 보유가치 측면의 음(-)의 영향이 더 크게 작용한 것으로 추정되었다. <그림 IV-7>은 전망에서도 생산 측면의 수익률은 대체로 자본투자 수익률을 높이는 방향으로 작용하지만, 보유가치 측면의 수익률은 이를 낮추는 방향으로 작용함을 나타낸다. 그리고 결과적으로는 보유가치 측면의 하방 영향이 전반적으로 크게 작용하면서 자본투자 수익률이 낮아지는 모습을 보인다. 이러한 점을 볼 때, 향후에도 실증 분석에서 나타났던 경향이 당분간 지속될 것으로 예상할 수 있다.

<그림 IV-9>는 연간 자본투자 수익률을 생산 및 보유가치 측면의 요인으로 구분하여 중위 전망 대비 격차를 나타내고 있다. 먼저, 생산 측면의 수익률을 보면, 고위와 중위의 차이(고-중)는 대부분 음(-), 저위와 중위의 차이(저-중)는 대부분 양(+)의 수치를 보이면서 저위, 중위, 고위의 순으로 높다는 점을 알 수 있다. 다음으로 보유가치 측면의 경우, 고위와 중위의 차이(고-중)는 대부분 양(+), 저위와 중위의 차이는 대부분 음(-)의 수치로 고위 전망에서 가장 높다. 따라서 고위 전망에서 생산 측면의 수익률이 낮기는 하지만, 보유가치 측면의 수익률이 한층 더 높기 때문에 고위 전망의 자본투자 수익률이 가장 높은 것으로 볼 수 있다.



나. 고연령층의 노동시장 참여
앞 절에서는 25~49세 인구에 대한 중위 전망을 기본으로 하여 해당 인구가 상위 또는 하위 전망에 따라 변화하는 경우와 비교해 보았다. 여기에서는 고연령층의 노동시장 참여가 증가하는 경우를 가정하여 자본투자 수익률을 전망해 보고자 한다. 인구 구조상 50세 이상 고연령층의 비중이 커지고, 보건의료 수준도 개선되어 경제활동 참가 기간이 길어질 수 있으므로 이러한 시나리오에 대한 분석도 상당한 의미가 있을 것으로 생각된다.

이러한 추세는 앞으로도 지속될 가능성이 있다. 보건의료 수준 개선과 함께, 최근의 청년층 교육 수준 향상34)도 향후 고연령층의 경제활동 참가율을 높이는 요인으로 작용할 수 있기 때문이다. 즉, 고연령 인구의 인적자본이 고도화되면서 동 연령층이 생산활동에서 유효하게 활용될 수 있는 여지가 과거에 비해 커질 수 있다. 아울러 우리나라보다 고연령층의 경제활동 참가율이 높은 선진국이 다수 존재한다는 점도 참고할 만한 사실이라 생각된다. 이는 <그림 IV-13>에 제시된 OECD 국가 내 55~64세 인구의 경제활동 참가율(2022년)을 통해 확인할 수 있다. 우리나라의 경우 해당 연령대의 경제활동 참가율은 70.3%로 OECD 평균보다 높지만, 독일(75.3%), 일본(80.1%), 스웨덴(81.7%) 등에 비해서는 낮고 그 격차도 다소 큰 편이다. 이러한 점을 볼 때 고연령층의 노동시장 참여 증가는 어느 정도 실현 가능성이 존재하는 시나리오라고 판단된다.


다. 여성의 노동시장 참여
본 절에서는 또 다른 가능성으로 여성의 노동시장 참여가 증가하는 경우를 고려해 보고자 한다. 잘 알려진 바와 같이, 우리나라 여성의 경제활동 참가율은 남성보다 상당히 낮은 수준이며36) 주요국에 비해서도 낮은 편이다. <그림 IV-15>는 OECD 국가들의 여성 경제활동 참가율(2021년)을 표시하고 있는데, 우리나라 여성의 참가율은 53.3%로 나타난다. 이는 OECD 평균인 55.5%을 하회하는 수준으로 OECD 내 백분위로는 하위 32%에 속한다. 그리고 상위 5개 국가37)의 평균(67.9%)과 비교하면 약 15%p의 큰 격차를 보인다.


라. 총요소생산성 변화
마지막으로 총요소생산성에 대한 시나리오로부터 산출된 결과에 대해 논의하고자 한다. III장에서 살펴본 바와 같이 우리나라의 총요소생산성 증가율(연평균)은 1980~1990년대에는 3.8%, 2000년 이후에는 2.4%로 낮아졌고, 최근에는 대체로 2% 내외의 수준을 보이고 있다. 기본 시나리오에서는 2010년 이후의 자료를 반영하여 매년 1.7% 증가하는 것으로 설정하였는데, 본 시나리오 분석에서는 20년간 점진적으로 1%까지 하락하거나 2%까지 상승하는 경우를 추가로 고려하였다. 여기에서 하방 시나리오(1%)는 우리나라의 기술 진보율의 전반적인 위상이 OECD 상위권에서 중위권으로 낮아지는 경우로 생각해 볼 수 있다.38) 그리고 상방 시나리오(2%)는 최근 3년간(2019~2021년)의 국내 총요소생산성 증가율 평균(1.9%)에 가까운 수준으로 수렴하는 경우에 해당한다.
<그림 IV-17>은 20년 후 총요소생산성 증가율이 2%(고) 및 1%(저)인 경우의 누적 자본투자 수익률을 보이고 있다. 이 결과에 따르면, 향후 20년간 누적수익률은 각각 64%(고) 및 20%(저)로 기본 시나리오와 대비할 때 각각15%p 및 29%p의 차이를 보인다. 이러한 격차는 향후 자본투자 수익률 흐름에 있어 인구뿐만 아니라 기술 발전의 영향도 결코 간과할 수 없다는 점을 보여준다.

Ⅴ. 요약 및 결론
본 연구에서는 이론적인 모형을 바탕으로 자본투자 수익률을 추정하고, 주식 수익률과의 관계에 대해 살펴보았다. 실증 분석 결과에 따르면, 자본투자 수익률은 주식 수익률의 장기 추이를 설명하는 데 유용하게 활용될 수 있음을 알 수 있었다. 이는 주가가 기업의 투자와 생산 등 실물 경제활동과 무관하지 않으며, 주식 수익률의 움직임을 설명하는 데 있어 이러한 배경에 대한 고찰이 필요하다는 점을 의미한다.
지난 40년여 간의 자료를 분석한 결과, 2000년 이후 자본투자 수익률은 이전에 비해 평균적으로 하락한 것으로 나타났다. 이는 고도 성장기가 저물고 저성장 국면으로 진입한 데 따른 결과로 생각될 수도 있다. 하지만, 자본투자 수익률의 구성 요소에 대해 세부적으로 살펴보면서 보다 흥미로운 결과를 발견할 수 있었다. 기간별로 비교해 볼 때, 2000년대 들어 보유가치 측면의 수익률은 전반적으로 하락하였지만, 생산 측면의 수익률은 소폭 상승했다는 점이 특징적으로 나타났다. 그리고 이 중 생산 측면의 수익률이 상승한 것은 자본재 가격의 하락이 미친 영향이 컸기 때문으로 분석되었다. 세부적으로 보면, 자본의 한계생산성은 지속적으로 하락하는 추세를 나타내면서 생산 측면의 수익률을 낮추는 요인으로 작용하였다. 반면, 자본재 가격은 1990년경부터 하락세가 두드러지면서 수익률을 높이는 요인으로 작용하여 상반된 양상을 보였다. 이러한 결과는, 추가 자본투입을 통한 생산량 증가폭은 감소하였지만, 자본재를 보다 저렴하게 구입할 수 있게 됨으로써 생산 측면의 수익률이 향상되었다는 점을 의미한다.
본 연구에서는 이러한 실증 분석과 함께, 여러 시나리오를 통해 향후 20년간의 자본투자 수익률을 전망해 보았다. 통계청의 중위 인구 전망을 이용한 시나리오 분석 결과에 따르면, 인구 증가율과 자본투자 수익률의 시계열이 상당히 유사한 방향성을 가지고 움직이는 특징을 보였다. 아울러 인구 수준별 시나리오에 따르면, 20년 후 고위와 저위 인구 시나리오에 따른 누적수익률은 중위 대비 ±20%p에 가까운 격차를 나타냈다. 이상의 결과들은 인구 변화가 구조적인 요인으로 작용하면서 그 전개 방향에 따라 자본투자 수익률이 크게 변화할 수 있다는 점을 시사한다.
위의 시나리오 분석은 인구를 제외한 연령별·성별 경제활동 참가 정도는 현재와 동일할 것이라는 가정을 바탕으로 한다. 하지만, 현실적으로는 인구 고령화, 인적 자본의 고도화, 노동시장 참여 여건 개선 등이 진행되면서 다른 전제가 필요할 수도 있다. 이러한 점을 고려하여 고연령층과 여성의 노동 공급이 확대되는 경우를 각각 가정한 시나리오에 대해 추가로 분석해 보았다. 결과에 따르면, 50~64세 인구와 여성의 노동 공급이 일정하게 증가하여 각각 7%p 및 10%p 확대되는 경우, 자본투자 수익률(누적)은 기본 시나리오 대비 24%p와 36%p 상승하는 것으로 전망되었다.
실물 경제뿐만 아니라 주식 시장의 성장을 위해서도 기술 진보와 생산성 향상의 중요성은 분명히 강조되어야 한다. 하지만 향후 당면하게 될 경제환경을 그려보면, 이러한 자명한 결론보다는 노동시장 참여 여건을 개선하여 기술 진보를 보완할 수 있는 가능성에 대해 주목할 필요가 있다. 특히, 앞서 고연령층 및 여성의 노동 공급 증가를 가정한 시나리오에서의 수익률은 20년 후 총요소생산성 증가율이 2% 수준까지 상승하는 경우보다 높은 것으로 나타났다. 2000년 이후 총요소생산성 증가율이 1980~1990년대의 절반 수준으로 낮아졌다는 점을 고려할 때, 총요소생산성 증가율 추세의 상승 전환은 쉽지 않은 과제이다. 이러한 의미에서 위의 결과는 노동시장에 대한 개선을 병행함으로써 기술 발전 둔화를 보완해 나가야 함을 시사한다.
고연령층과 여성의 노동시장 참여는 가용 노동자원을 확대할 수 있는 주요 원천이지만, 이를 단기간에 크게 끌어올리는 데에는 한계가 있을 수 있다. 하지만, 본 연구의 시나리오 분석은 점진적인 개선도 중요한 동력으로 작용하면서 자본투자 수익률을 크게 제고할 수 있다는 점을 함축한다. 아울러 고연령층과 여성의 경제활동이 활성화된 주요국의 사례에 비추어 볼 때, 효율적인 정책 개발과 실행이 뒷받침된다면 긍정적인 시나리오가 현실화될 수 있을 것이다.
1) 일반균형 모형에서 확률적 할인인자
2) 일차적인 의미는 투자에 사용된 최종재 1단위(분자, 1)를 최종재 1단위 투자로 추가된 자본량
3) 엄밀하게는 보유한 자본에서 얻게 될 미래의 배당 가치를 평가한 것이다.
4) Restroy and Rockinger(1994)의 첫 번째 명제(proposition 1)에서 생산함수와 자본조정비용이 선형동차 함수(linearly homogeneous function)이면 두 수익률 간에 동일성이 성립한다는 결과로, 모형의 콥-더글라스 생산함수와 식 (3)의 자본조정비용은 해당 조건을 만족한다. 참고를 위해 <부록>에 도출 과정을 수록하였다.
5) 자본 대 투자 비율
6) 생산함수의 모수
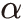 는 2010년 이후 민간 부문의 부가가치 대비 영업잉여 비율의 평균,
는 2010년 이후 민간 부문의 부가가치 대비 영업잉여 비율의 평균, 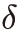 는 시산 결과(6%: 조태형 등(2012))와 기존 문헌(10%: 배병호 등(2018))의 평균을 적용하였다.
는 시산 결과(6%: 조태형 등(2012))와 기존 문헌(10%: 배병호 등(2018))의 평균을 적용하였다.7) 아울러
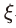 가 무한대에 가까워지면 자본재와 최종재의 가격이 같아지지만,
가 무한대에 가까워지면 자본재와 최종재의 가격이 같아지지만, 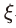 이 유한한 양수이면 자본재와 최종재의 가격이 달라지게 된다.
이 유한한 양수이면 자본재와 최종재의 가격이 달라지게 된다.8) GMM에서는 도구 변수(instrumental variable)로 과거 3년간 민간 소비 증가율의 평균을 사용하였다.
9) 지수 편제와 관련된 자세한 내용은 한국은행(2009)을 참조하기 바란다.
10) 주거용 건물은 민간의 주거 서비스를 위해 소비되므로 기업의 생산에 활용되는 자본재로 보기는 어렵다. Farhi and Guorio(2018)도 본고와 동일한 방식으로 민간 투자를 측정하였다.
11) <부록>에는 보다 구체적인 내용과 함께 산출된 거시지표의 기술 통계량, 총요소생산성 계산 방식, 성장회계에 따른 요인별 기여도 등이 수록되어 있다.
12) 귀무가설
13) 추정에서 KOSPI의 지수수익률 대신 배당의 재투자가 반영된 총수익률(total return)을 사용하는 경우에도 실증 분석 결과에는 큰 차이가 없는 것으로 나타났다. <부록>에 총수익률을 이용한 추정 결과가 제시되어 있다.
14) 식 (6)은
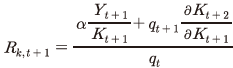 이며
이며 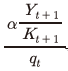 은 생산 측면,
은 생산 측면, 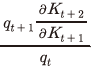 는 보유가치 측면의 수익률에 해당한다.
는 보유가치 측면의 수익률에 해당한다.15) 보다 엄밀하게는 외환위기 발생(1997년) 전후를 기준으로 평균이 유의하게 하락한 것으로 나타난다.
16) <그림 III-5>의 자본재 가격은 모형과 동일한 개념에 따라 자본재의 가격을 최종재(민간 소비)의 가격으로 나눈 상대가격이다. 자본재의 가격은 생산용 민간 자본투자(주거용 건물 및 재고 제외)에 속하는 각 항목의 GDP 디플레이터와 물량 지표를 이용하여 연쇄 라스파이레스 방식으로 산출한 것이다.
17) OECD 국가들의 경우 민간 부문만을 대상으로 한 자본생산성 변화율 자료 확보가 어려워 정부 부문까지 포함된 자료를 사용하였다. 하지만, 동일한 기준(정부 부문 포함)으로 산출된 자료로 비교하더라도 이러한 평가는 달라지지 않는다. 해당 결과는 <부록 3>에 제시되어 있다.
18) OECD 국가들의 자료에는 <그림 III-7>과 유사하게 정부 부문까지 포함되어 있지만, 동일한 기준(정부 부문까지 포함)으로 산출된 자료로 비교하더라도 이러한 평가는 달라지지 않는다. 해당 결과에 대해서는 <부록 3>에 제시되어 있다.
19) <그림 III-11>에 별도로 추세선을 표시하지는 않았지만, OECD 국가들의 중위수와 평균은 모두 유의하게 하락하는 모습을 나타낸다.
20) 엄밀하게는 한계 증가분이라는 표현이 맞지만, 자본은 감가상각과 자본조정비용에 의해 감소하게 되므로 직관적인 의미에 보다 가까운 잔존도라는 표현을 사용하였다.
21) 자본조정비용이 존재하지 않는 경우에는
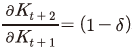 가 된다.
가 된다.22)
23) 2000년 전후 평균 측면에서 보면 자본재 가격 변화율도 일부 영향을 미쳤지만, 자본 잔존도가 추세적으로 하락한 영향이 주도하였으므로 여기에 초점을 맞추었다.
24) t+1부터 t+5시점까지의 I/K 비율 평균을 종속변수, t-4부터 t시점까지의 TFP 증가율 평균을 독립변수로 한 예측식(predictability regression)에서 TFP 증가율은 I/K 비율을 유의하게 예측하며 설명력(R2=0.66)도 매우 높은 것으로 나타났다.
25) 균형 경로에서 소비와 GDP는 동일한 변화율을 따르는 것으로 가정한다.
26)
27) 2024년 이후 기간의 전망을 위해서는 2023년의 투자가 필요한데, 이 값은 2024년의 민간 총생산(GDP) 증가율에 대한 자체 전망치(2%)를 적용하여 산출하였다. 즉, 동 성장률에 상응하는 2024년의 자본량을 도출하면 2023년의 투자가 계산된다.
28) 노동투입량 추세의 경우, 비선형(3차식) 추세의 설명력(R2=0.94)이 선형 추세(R2=0.69)보다 훨씬 높아 비선형식을 이용하였다. 아울러 2차식을 이용할 경우에도 정점 도달 시기에는 큰 차이가 없다.
29) 소비자물가상승률로 실질화된 통안증권(1년) 수익률의 평균을 사용하였다.
30) 식 (4)에 일반화 적률법을 적용하여 추정한 결과를 활용하였다. 추정치의 95% 신뢰구간은 (0.61, 3.60)인데, 시나리오 분석에서 사용된 값은 점 추정치(2.1)에 가까운 수치이다. 박명호·오종현(2015)에서도 본고와 동일한 위험회피도가 사용되었다.
31) 저위 전망에서는 필요 자본 규모가 더 작기 때문에 자본재의 가치가 상대적으로 낮게 평가되는 것으로 해석할 수 있다.
32) 이는 투자 규모가 크게 축소된 영향이 누적되어 중위나 고위 시나리오에 비해 자본축적도가 상대적으로 낮아진 데 기인한 것으로 볼 수 있다.
33) 즉, 고위 전망에서는 자본재 수요(투자)가 상대적으로 높기 때문에 가격 하락폭이 비교적 완만한 모습을 보이고, 자본의 잔존도도 높게 유지된다는 점이다.
34) 우리나라 25~34세 인구의 고등(대학)교육 이수율은 2000년 38.5%에서 2021년 69.3%로 대폭 증가하였다. 2021년 기준 동 연령대의 고등교육 이수율은 OECD 중 1위이며 OECD 평균(47.1%)을 20%p 이상 상회한다.
35) OECD 통계에서는 55~64세 기준 자료만 가용하기 때문에 이 연령대의 격차를 기준으로 하였다.
36) 2022년 기준 남성과 여성의 경제활동 참가율은 각각 73.5% 및 54.6%로 20%p에 가까운 격차가 존재한다.
37) 상위 5개국은 아이슬란드(75.1%), 스웨덴(70.9%), 뉴질랜드(66.1%), 핀란드(64.6%), 네덜란드(62.8%)이다.
38) 앞 장에서 언급한 바와 같이 OECD의 총요소생산성 증가율에는 정부 부문이 포함되어 있어 정확한 직접 비교가 어렵다는 문제가 있다. 다만, 미국의 민간 부문(business sector) 총요소생산성 증가율과 연계해서 생각할 때 위와 같은 추론이 가능하다. 미국의 1980~2021년 중 민간 부문 총요소생산성 증가율의 평균은 약 0.9%로 전제치의 하한인 1%에 가까운데, OECD 그룹 내에서 미국의 총요소생산성 증가율(정부 포함)은 중위 수준에 해당한다. 단, 이는 과거 자료를 기준으로 순위를 비교한 것으로, 1%로 낮아지는 것이 향후 미국의 총요소생산성 변화율에 수치상 근접하게 될 것이라는 의미가 아님을 밝혀 둔다. 여기에서 미국 민간 부문의 수치는 샌프란시스코 연준(https://www.frbsf.org/economic-research/indicators-data/)에서 제공되는 자료(Solow의 잔차, 계열명은 ‘dtfp’)이다.
39) 물리력을 보조하는 로봇 등이 일반화되는 경우를 생각할 수 있다.
40) Restroy & Rockinger(1994)의 보조 정리 1(Lemma 1)을 참조할 수 있다.
41) 통계청의 민간 부문 종사자수와 평균 근로시간을 곱한 수치이다.
42) 해당 기업 목록과 자료 분석에 관련된 조언을 주신 자본시장연구원 김준석 박사께 감사드린다.
참고문헌
박명호·오종현, 2015, 『조세재정정책의 거시경제적 효과 분석을 위한 DSGE 모형 구축: GIMF 모형의 이해와 활용』.
배병호·유진혁·지정구, 2018, 경제전망 및 정책분석을 위한 BOKDSGE 모형 개선 결과, 『조사통계월보』 2018년 1월호.
조태형·이병탁·도경탁, 2012, 자산별 내용연수의 추정에 관한 연구, 『국민계정리뷰』 2012년 1호.
한국거래소, 2018, 『신규 총수익지수 7종 발표』.
한국은행, 2009, 『연쇄가중 경제성장률 이해』.
한국은행, 2020, 『한국의 국민대차대조표 해설』.
Boldrin, M., Christiano, L.J., Fisher, J.D.M, 2001, Habit persistence, asset returns, and the business cycle. American Economic Review 91, 149–66.
Christiano, L.J., Fitzgerald T.J., 2003, The band pass filter, International Economic Review 44(2), 435-465.
Cochrane, J.H, 1991, Production-based asset pricing and the link between stock returns and economic fluctuations, Journal of Finance 46(1), 209-237.
Croce, M.M., 2014, Long-run productivity risk: A new hope for production-based asset pricing? Journal of Monetary Economics 66, 13-31.
Farhi, E., Guorio, F., 2018, Accounting for macro-finance trends: Market power, intangibles, and risk premia, Brookings Papers on Economic Activity, Fall 2018.
Hansen, L.P., Singleton, K.J., 1983, Stochastic consumption, risk aversion, and the temporal behavior of asset returns, Journal of Political Economy 91(2), 249-265.
Hayashi, F., 1982, Tobin's marginal q and average q: A neoclassical interpretation, Econometrica 50(1), 213-224.
International Monetary Fund, 2019, The price of capital goods: A driver of investment under threat? World Economic Outlook, April 2019.
Jermann, U., 1998, Asset pricing in production economics, Journal of Monetary Economics 41, 257–75.
Kaltenbrunner, G., Lochstoer, L.A., 2010, Long-run risk through consumption smoothing, Review of Financial Studies 23(8), 3190-3224.
Organisation for Economic Co-operation and Development, 2001, Measurement of aggregate and industry-level productivity growth, Measuring Productivity-OECD Manual.
Restoy, F., Rockinger, M., 1994, On stock market returns and returns on investment, Journal of Finance 49, 543–56.
<부록>
1. 주식 수익률과 자본투자 수익률의 이론적 관계
기업 가치를 배당과 계속 가치의 항으로 나타내면, 가치 함수는 다음과 같이 표현할 수 있다.
위 식에서
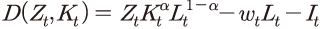 이며 계속 가치는 배당 후 주가에 해당하므로
이며 계속 가치는 배당 후 주가에 해당하므로 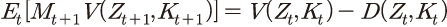 로 나타낼 수 있다. 따라서 주식 수익률
로 나타낼 수 있다. 따라서 주식 수익률 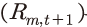 은 다음과 같이 표현된다.
은 다음과 같이 표현된다.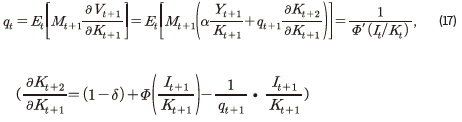
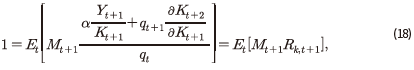
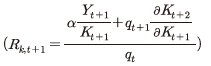
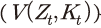 는 자본
는 자본 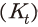 에 선형성40을 가지므로 다음이 성립한다.
에 선형성40을 가지므로 다음이 성립한다.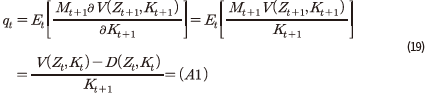
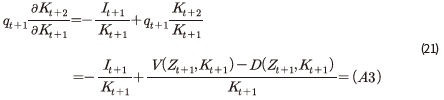
먼저, 민간 총생산을 산출하는 데에는 한국은행의 경제통계 시스템(ECOS)에 수록된 「2.1.2.1.3. 경제활동별 GDP 및 GNI(명목)」 및 「2.1.2.1.4. 경제활동별 GDP 및 GNI(실질)」자료를 이용한다. 여기에서는 기본적으로 정부 부문을 제외한 세부문의 생산액을 대상으로 한다. 각 세부문의 명목 생산액을 실질 생산액으로 나누어 가격 디플레이터를 구하고, 연쇄 라스파이레스 방식을 통해 합산함으로써 민간 부문의 실질 GDP를 계산한다.
투자는 ECOS의 「2.1.6.2.1. 주체별 총자본형성(명목)」에 제공되는 민간 부문의 총자본형성(명목)에서 주거용 투자를 차감한 값을 연쇄 라스파이레스 가격 지수로 실질화하여 산출한다. 여기에는 비주거용 건물, 토목건설, 운송장비, 기계류, 연구개발, 기타 지식재산생산물이 포함된다. 가격 디플레이터는「2.1.6.1.3. 자본재형태별 총자본형성(명목)」 및 「2.1.6.1.4. 자본재형태별 총자본형성(실질)」에서 주거용 건물 및 재고를 제외한 투자 항목의 명목 및 실질 금액을 이용하여 산출하게 된다.
자본 스톡은 ECOS에서 국민대차대조표 자료인 「2.4.5.1. 제도부문별 생산자본스톡
(명목)」 및 「2.4.5.2. 제도부문별 생산자본스톡(실질)」중 민간 부문의 자본 스톡 자료를 이용하였다. 투자와 마찬가지로 주거용 건물을 제외한 고정자산의 명목 및 실질 금액을 이용하여 가격 디플레이터를 구하고, 연쇄 라스파이레스 방식으로 비주거용 자본 스톡의 실질액을 산출한다.
전술한 연쇄 라스파이레스 방식에 따른 t기의 실질(물량,
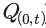 ) 및 가격 지수
) 및 가격 지수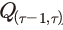 ,
, 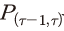 를 각각 이용하여 식 (23) 및 (24)와 같이 계산된다.
를 각각 이용하여 식 (23) 및 (24)와 같이 계산된다.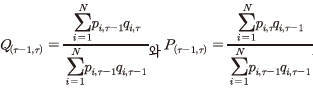 로 정의되며 하첨자
로 정의되며 하첨자아래의 <부록 그림 1>에는 이상의 방법으로 산출한 민간 부문의 총생산, 비주거용 투자 및 자본 스톡의 실질액(로그)과 자본 대비 투자 비율(I/K)이 나타나 있다. 아울러 <부록 표 1>에는 민간 총생산, 투자, 자본의 증가율과 자본 대비 투자 비율에 대한 주요 기술 통계량이 제시되어 있다.


총요소생산성의 변화는 식 (1)에 제시된 콥-더글라스 생산함수

총수익률 지수의 공식 통계(한국거래소 발표)는 2011년부터 존재한다. 이전 기간에 대해서는 상장회사협의회의 자료(TS2000)를 이용하여 KOSPI 지수 내 기업별 배당을 집계하여 연장한 자료를 사용하였다. 단, TS2000에는 상장폐지 기업들의 상장폐지 이후 기간의 자료, 신규 상장 기업들의 상장 이전 기간의 자료, 기업인수목적회사(SPAC) 및 외국 기업들의 자료 등이 포함되어 있어 이들은 집계에서 제외하였다.42
아래의 <부록 표 2>와 <부록 표 3>은 총수익률을 이용하여 본문과 동일한 방법으로 추정한 자본조정비용의 모수 및 자본투자 수익률과 주식 수익률간 관계를 보여주고 있다. 아울러 <부록 그림 3>과 <부록 그림 4>는 자본투자 수익률과 주식 수익률의 연간 자료, 두 수익률의 5년 이동 평균과 중장기 성분(Christiano-Fitzgerald 필터 이용)의 추이를 나타내고 있다.




아래 <부록 그림 5>와 <부록 그림 6>은 OECD 국가들을 대상으로 정부 부문이 포함된 자본의 한계생산성 변화율과 총요소생산성 변화율을 각각 나타내고 있다.